题目内容
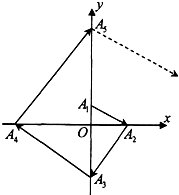如图所示，点列{An}满足：|| OA1 |
| OAi+1 |
| OAi |
| OA1 |
| OA2 |
| OA2014 |
| A、（22014-1，0） | ||||
| B、（22016-1，22015-1） | ||||
C、（
| ||||
D、（
|
考点：等比数列的通项公式,向量加减混合运算及其几何意义
专题：点列、递归数列与数学归纳法,平面向量及应用
分析：由于点列{An}满足：|
|=1，|
|=2|
|+1，设an=|
|，则a1=1，an+1=2an+1，变形为an+1+1=2（an+1），可知；数列{an+1}是等比数列，利用通项公式可得an=2n-1．由于Ai均在坐标轴上（i∈N*），且A4n-3，A4n-2，A4n-1，A4n，（n∈N*）分别在y轴的正半轴，x轴的正半轴，y轴的负半轴，x轴的负半轴．
可得向量
+
+…+
的横坐标=a2-a4+a6-a8+…+a2010-a2012+a2014，向量
+
+…+
的纵坐标=a1-a3+a5-a7+…+-a2011+a2013，再利用等比数列的前n项和公式即可得出．
| OA1 |
| OAi+1 |
| OAi |
| OAi |
可得向量
| OA1 |
| OA2 |
| OA2014 |
| OA1 |
| OA2 |
| OA2014 |
解答：
解：∵点列{An}满足：|
|=1，|
|=2|
|+1，
设an=|
|，则a1=1，an+1=2an+1，化为an+1+1=2（an+1），
∴数列{an+1}是等比数列，
∴an+1=(a1+1)•2n-1=2n．
∴an=2n-1．
由于Ai均在坐标轴上（i∈N*），
且A4n-3，A4n-2，A4n-1，A4n，分别在y轴的正半轴，x轴的正半轴，y轴的负半轴，x轴的负半轴．
∴向量
+
+…+
的横坐标=a2-a4+a6-a8+…+a2010-a2012+a2014
=（22-1）-（24-1）+（26-1）-（28-1）+…+（22010-1）-（22012-1）+（22014-1）
=22-24+26-28+…+22010-22012+22014-1
=
-1
=
．
同理可得向量
+
+…+
的纵坐标=a1-a3+a5-a7+…+-a2011+a2013=
．
∴向量
+
+…+
=(
，
)．
故选：D．
| OA1 |
| OAi+1 |
| OAi |
设an=|
| OAi |
∴数列{an+1}是等比数列，
∴an+1=(a1+1)•2n-1=2n．
∴an=2n-1．
由于Ai均在坐标轴上（i∈N*），
且A4n-3，A4n-2，A4n-1，A4n，分别在y轴的正半轴，x轴的正半轴，y轴的负半轴，x轴的负半轴．
∴向量
| OA1 |
| OA2 |
| OA2014 |
=（22-1）-（24-1）+（26-1）-（28-1）+…+（22010-1）-（22012-1）+（22014-1）
=22-24+26-28+…+22010-22012+22014-1
=
| 4[(-4)1007-1] |
| -4-1 |
=
| 22016-1 |
| 5 |
同理可得向量
| OA1 |
| OA2 |
| OA2014 |
| 22015-3 |
| 5 |
∴向量
| OA1 |
| OA2 |
| OA2014 |
| 22016-1 |
| 5 |
| 22015-3 |
| 5 |
故选：D．
点评：本题考查了等比数列的通项公式、前n项和公式、向量的运算等基础知识与基本技能方法，考查了分类讨论和数形结合的思想方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
设随机变量ξ～N（3，σ2），若P（ξ≥7）=0.16，则P（-1≤ξ≤7）=（ ）
| A、0.84 | B、0.68 |
| C、0.32 | D、0.16 |
已知tanθ=2，则
=（ ）
2sin2(θ-
| ||
| 1+cos2θ |
A、
| ||
| B、1 | ||
C、
| ||
D、-
|
若不等式a+2b+3＞（
+2
）λ对任意正数a，b恒成立，则实数λ的取值范围为（ ）
| a |
| b |
| A、（-∞，3） | ||
| B、（-∞，2） | ||
| C、（-∞，1） | ||
D、（-∞，
|
已知二元函数f（x，θ）=
（x∈R，θ∈R），则f（x，θ）的最大值和最小值分别为（ ）
| xcosθ |
| x2+xsinθ+2 |
A、
| ||||||||
B、
| ||||||||
C、2
| ||||||||
D、2
|