题目内容
已知定义在R上的函数y=f（x）满足f（x+2）=f（x），当-1＜x≤1 时，f（x）=x3 则函数y=f（x）+log
|x|的零点的个数（ ）
| 1 |
| 5 |
| A、3 | B、4 | C、5 | D、6 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：根据题意，由函数零点的判断方法，函数g（x）=f（x）+log
|x|的零点个数，即函数y=f（x）与y=log5|x|的交点的个数，由函数图象的变换，分别做出y=f（x）与y=log5|x|的图象，分析其交点个数，即可得答案．
| 1 |
| 5 |
解答：
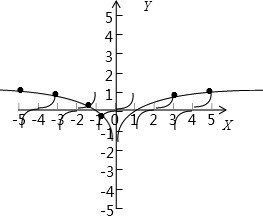解：根据题意，函数y=f（x）+log
|x|的零点个数，即函数y=f（x）与y=-log
|x|=log5|x|的交点的个数；
f（x+2）=f（x），函数f（x）是周期为2的周期函数，
又由当-1＜x≤1时，f（x）=x3，据此可以做出f（x）的图象，
y=log5|x|是偶函数，当x＞0时，y=log5x，则当x＜0时，y=log5（-x），做出y=log5|x|的图象，
结合图象分析可得：函数y=f（x）与y=log5|x|有6个交点，
则g（x）=f（x）-log5|x|有6个零点，
故选：D
解：根据题意，函数y=f（x）+log| 1 |
| 5 |
| 1 |
| 5 |
f（x+2）=f（x），函数f（x）是周期为2的周期函数，
又由当-1＜x≤1时，f（x）=x3，据此可以做出f（x）的图象，
y=log5|x|是偶函数，当x＞0时，y=log5x，则当x＜0时，y=log5（-x），做出y=log5|x|的图象，
结合图象分析可得：函数y=f（x）与y=log5|x|有6个交点，
则g（x）=f（x）-log5|x|有6个零点，
故选：D
点评：本题考查函数图象的变化与运用，涉及函数的周期性，对数函数的图象等知识点，关键是作出函数的图象，由此分析两个函数图象交点的个数．
练习册系列答案
相关题目
设随机变量ξ～N（3，σ2），若P（ξ≥7）=0.16，则P（-1≤ξ≤7）=（ ）
| A、0.84 | B、0.68 |
| C、0.32 | D、0.16 |
从数字0，1，2，3，…，9中，按由小到大的顺序取出a1，a2，a3，且a2-a1≥2，a3-a2≥2，则不同的取法有（ ）
| A、20种 | B、35种 |
| C、56种 | D、60种 |
直线xcosα-y+1=0的倾斜角的取值范围是（ ）
A、[
| ||||||||
B、[0，
| ||||||||
C、[-
| ||||||||
D、[
|
已知条件p：函数f（x）=ax-2b+2 对于任意的x∈[-1，1]恒有f（x）≥0，若对任意的一个实数a∈[-2，2]，一个实数 b∈[0，2]，则满足条件P的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知tanθ=2，则
=（ ）
2sin2(θ-
| ||
| 1+cos2θ |
A、
| ||
| B、1 | ||
C、
| ||
D、-
|
若不等式a+2b+3＞（
+2
）λ对任意正数a，b恒成立，则实数λ的取值范围为（ ）
| a |
| b |
| A、（-∞，3） | ||
| B、（-∞，2） | ||
| C、（-∞，1） | ||
D、（-∞，
|