题目内容
已知集合M={(x,y)|f(x,y)=0},若对任意P1(x1,y1)∈M,均不存在P2(x2,y2)∈M使得x1x2+y1y2=0成立,则称集合M为“好集合”,下列集合为“好集合”的是( )
| A、M={(x,y)|y-lnx=0} | ||
B、M={(x,y)|y-
| ||
| C、M={(x,y)|(x-2)2+y2-2=0} | ||
| D、M={(x,y)|x2-2y2-1=0} |
考点:子集与交集、并集运算的转换
专题:集合
分析:根据已知条件知道,集合M中不存在P1,P2,使OP1⊥OP2,O为坐标原点,所以判断哪个选项中的集合M,不含P1,P2,使OP1⊥OP2即可.
解答:
解:由x1x2+y1y2=0得OP1⊥OP2,即存在两点与原点连线互相垂直;
A.取(e,1)∈M,(
,-1)∈M,有e•
+1•(-1)=0;
B.取(2,2),(-2,2)∈M,有2•(-2)+2•2=0;
C.取(1,1),(1,-1),有1•1+1•(-1)=0;
D.x2-2y2=1,渐近线方程为:y=±
x,容易知道这两条渐近线夹角小于90°,所以不存在两点和原点的连线相互垂直,即该选项正确.
故选D.
A.取(e,1)∈M,(
| 1 |
| e |
| 1 |
| e |
B.取(2,2),(-2,2)∈M,有2•(-2)+2•2=0;
C.取(1,1),(1,-1),有1•1+1•(-1)=0;
D.x2-2y2=1,渐近线方程为:y=±
| ||
| 2 |
故选D.
点评:考查元素与集合的关系,描述法表示集合,已知两直线斜率k1,k2,k1•k2=-1时这两直线垂直.

练习册系列答案
相关题目
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
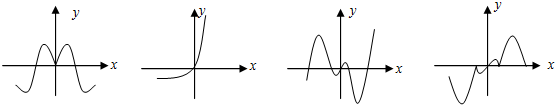
则按照从左到右图象对应的函数序号安排正确的一组是( )
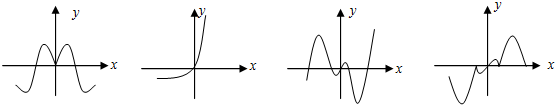
则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |
已知f(x)是R上的奇函数,且f(x+4)=f(x),当x∈(0,2)时,f(x)=x2,则f(7)的值为( )
| A、-1 | B、4 | C、1 | D、0 |
若x>0,y>0且2x=(
)2y-1,则
+
的最小值为( )
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2
| ||
| C、2 | ||
D、3+2
|
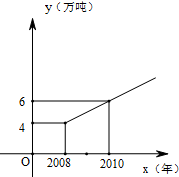 某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查结果分析显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升,y与x之间的关系如图所示.
某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查结果分析显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随着时间x(年)逐年成直线上升,y与x之间的关系如图所示.