题目内容
19.已知O,F分别为双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的中心和右焦点,点G,M分别在E的渐近线和右支,FG⊥OG,GM∥x轴,且|OM|=|OF|,则E的离心率为( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $\sqrt{2}$ |
分析 设M(m,n),则G($\frac{an}{b}$,n),利用FG⊥OG,求出n,可得m,利用|OM|=|OF|,求出E的离心率.
解答 解:设M(m,n),则G($\frac{an}{b}$,n),
∵FG⊥OG,∴$\frac{n}{\frac{an}{b}-c}•\frac{b}{a}=-1$,∴n=$\frac{ab}{c}$,
∴$\frac{{m}^{2}}{{a}^{2}}-\frac{{a}^{2}}{{c}^{2}}$=1,∴m2=$\frac{{a}^{2}{c}^{2}+{a}^{4}}{{c}^{2}}$,
∵|OM|=|OF|,∴$\frac{{a}^{2}{c}^{2}+{a}^{4}}{{c}^{2}}$+$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$=c2,
∴2a2=c2,∴e=$\frac{c}{a}$=$\sqrt{2}$,
故选D.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,确定M的坐标是关键.

练习册系列答案
相关题目
10.如图是一个正方体被切掉部分后所得几何体的三视图,则该几何体的体积为( )
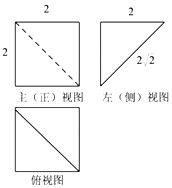

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{{8\sqrt{2}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
7.将函数f(x)=cos2ωx的图象向右平移$\frac{3π}{4ω}$个单位,得到函数y=g(x)的图象,若y=g(x)在$[-\frac{π}{4},\frac{π}{6}]$上为减函数,则正实数ω的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
4.已知集合A={0,2,4,6},B={x∈N|2x<33},则集合A∩B的子集个数为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 4 |
9.下列函数中,既是偶函数又在区间(0,+∞)上单调递减的是( )
| A. | y=|x| | B. | y=x-2 | C. | y=ex-e-x | D. | y=-x+1 |
 设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.
设抛物线E:y2=2px(p>0)上的点M(x0,4)到焦点F的距离|MF|=$\frac{5}{4}$x0.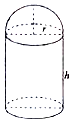 某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.