题目内容
8.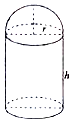 某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.
某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r.
分析 (Ⅰ)利用容积为72π立方米,列出$72π=\frac{{2π{r^3}}}{3}=π{r^2}h$,得到$h=\frac{72}{r^2}-\frac{2r}{3}≥2r$,然后求解建造费用的函数解析式.
(Ⅱ)利用导函数,判断单调性求解最值即可.
解答 (本小题满分12分)
解:(Ⅰ)由容积为72π立方米,得$72π=\frac{{2π{r^3}}}{3}=π{r^2}h$.…(2分)
$h=\frac{72}{r^2}-\frac{2r}{3}≥2r$,解得0<r≤3,…(4分)
又圆柱的侧面积为$2πrh=2πr({\frac{72}{r^2}-\frac{2r}{3}})$,
半球的表面积为2πr2,
所以建造费用$y=\frac{288π}{r}+\frac{{16π{r^2}}}{3}$,定义域为(0,3].…(6分)
(Ⅱ)$y'=16π({\frac{18}{r}+\frac{r^2}{3}})'=32π\frac{{({r^3}-27)}}{{3{r^2}}}$,…(8分)
又0<r≤3,所以y'≤0,所以建造费用$y=\frac{288π}{r}+\frac{{16π{r^2}}}{3}$,
在定义域(0,3]上单调递减,所以当r=3时建造费用最小.…(12分)
点评 本题考查函数的导数的应用,函数的最值的求法,实际问题的处理方法,考查转化思想以及计算能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
19.已知O,F分别为双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的中心和右焦点,点G,M分别在E的渐近线和右支,FG⊥OG,GM∥x轴,且|OM|=|OF|,则E的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | $\sqrt{2}$ |
16.曲线y=2x2-x在点(0,0)处的切线方程为( )
| A. | x+y=0 | B. | x-y=0 | C. | x-y+2=0 | D. | x+y+2=0 |
3.设函数f(x)=ex(sinx-cosx)(0≤x≤4π),则函数f(x)的所有极大值之和为( )
| A. | e4π | B. | eπ+e2π | C. | eπ-e3π | D. | eπ+e3π |
13.不等式2x2-x-3>0的解集为( )
| A. | {x|x<2或x>3} | B. | {x|x<-1或x>3} | C. | {x|x<-1或x>$\frac{3}{2}\}$ | D. | {x|x<1或x>$\frac{3}{2}\}$ |
17.若函数y=3sin(2x+φ)(-π<φ<0)的图象向左平移$\frac{π}{6}$后得到的图象关于y轴对称,|φ|=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |