题目内容
10．如图是一个正方体被切掉部分后所得几何体的三视图，则该几何体的体积为（ ）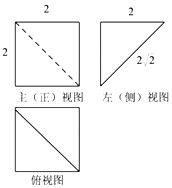
| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | $\frac{{8\sqrt{2}}}{3}$ | D． | $\frac{{4\sqrt{2}}}{3}$ |
分析 该几何体为正方体先切割得到的三棱柱后，再切割得到四棱锥，由此能求出该几何体的体积．
解答 解：
由三视图可知：
该几何体为正方体先切割得到的三棱柱后，
再切割得到四棱锥S-ABCD，如图所示，
则其体积为：
VS-ABCD=$\frac{1}{3}×{S}_{正方形ABCD}×AS$=$\frac{1}{3}×2×2×2$=$\frac{8}{3}$．
故选：B．
点评 本题考查该几何体的体积的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
如图：在斜三棱柱ABC-A1B1C1中，四边形ABB1A1是菱形，四边形CBB1C1是矩形，AC=5，CB=3，AB=4，∠A1AB=60°．
5．函数f（x）的定义域为D，若对于任意x1，x2∈D，当x1＜x2时都有f（x1）≤f（x2），则称函数f（x）在D上为非减函数，设f（x）在[0，1]为非减函数，且满足以下三个条件；①f（0）=0；②f（$\frac{x}{3}$）=$\frac{1}{2}$f（x）；③f（1-x）=1-f（x），则f（$\frac{1}{3}$）+f（$\frac{1}{8}$）等于（ ）
| A． | $\frac{1}{128}$ | B． | $\frac{1}{256}$ | C． | $\frac{1}{512}$ | D． | $\frac{3}{4}$ |
2．已知变量x，y成负相关，且由观测数据算得样本平均数$\overline x=3$，$\overline y=3.5$，则由该观测数据算得的线性回归方程可能是（ ）
| A． | y=0.4x+2.3 | B． | y=2x+2.4 | C． | y=-2x+9.5 | D． | y=-0.4x+4.4 |
19．已知O，F分别为双曲线E：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的中心和右焦点，点G，M分别在E的渐近线和右支，FG⊥OG，GM∥x轴，且|OM|=|OF|，则E的离心率为（ ）
| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{6}}}{2}$ | C． | $\frac{{\sqrt{7}}}{2}$ | D． | $\sqrt{2}$ |