题目内容
若等比数列{an}中a4=1，则a3+a4+a5的取值范围是（ ）
| A、（-∞，-1] |
| B、（-∞，0）∪（1，+∞） |
| C、[3，+∞） |
| D、（-∞，-1]∪[3，+∞） |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：等比数列{an}中a4=1，可得a3+a4+a5=
+1+q，结合
+q∈（-∞，-2]∪[2，+∞），即可得出结论．
| 1 |
| q |
| 1 |
| q |
解答：
解：设等比数列的公比为q，则
∵等比数列{an}中a4=1，
∴a3+a4+a5=
+1+q，
∵
+q∈（-∞，-2]∪[2，+∞），
∴
+1+q∈（-∞，-1]∪[3，+∞），
故选：D．
∵等比数列{an}中a4=1，
∴a3+a4+a5=
| 1 |
| q |
∵
| 1 |
| q |
∴
| 1 |
| q |
故选：D．
点评：本题考查等比数列的通项，考查基本不等式的运用，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
下列函数中，最小值为4的是（ ）
A、y=x+
| ||
B、y=sinx+
| ||
| C、y=3x+4•3-x | ||
| D、y=log3x+4logx3 |
学校为了了解高二年级教学情况，对清北班、重点班、普通班、艺术班的学生做分层抽 样调查，假设学校高二年级总人数为N，其中清北班有学生144人，若在清北班、重点班、普通班、艺术班抽取的人数分别为18，66，53，24，则总人数N为（ ）
| A、801 | B、1 288 |
| C、853 | D、912 |
设函数f（x）=
x3+
cosθx2+sinθ，其中θ∈[0，
]，则导数f′（
）的取值范围是（ ）
| 4sinθ |
| 3 |
| 3 |
| 5π |
| 12 |
| 1 |
| 2 |
| A、[-2，2] | ||||
B、[
| ||||
C、[
| ||||
D、[
|
函数f（x）=cos（
-x）cosx是（ ）
| π |
| 2 |
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
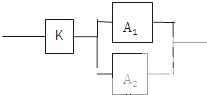如图．用K，A1，A2分别不同的原件连接成一个系统．当K正常工作且A1和A2正常工作的概率是0.9，0.8，0.8则系统正常工作的概率为（ ）| A、0.960 | B、0.864 |
| C、0.72 | D、0.576 |