题目内容
16.已知四边形ABCD中,AB=2,AD=4,BC=6,CD=2,3$\overrightarrow{AB}$•$\overrightarrow{AD}$+2$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,则四边形ABCD的面积为5$\sqrt{3}$.分析 由向量式和已知数据可得cosB=-cosD,由余弦定理可得AC2=40-24cosB,AC2=20+16cosB,解方程组可得cosB=$\frac{1}{2}$,进而可得sinB=$\frac{\sqrt{3}}{2}$,由三角形的面积公式可得
解答  解:∵3$\overrightarrow{AB}$•$\overrightarrow{AD}$+2$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,
解:∵3$\overrightarrow{AB}$•$\overrightarrow{AD}$+2$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,
∴3|$\overrightarrow{AB}$||•$\overrightarrow{AD}$|cosA+2|$\overrightarrow{CB}$|•|$\overrightarrow{CD}$|cosC=0
又∵AB=2,AD=4,BC=6,CD=2,
∴cosA=-cosC,
∵0<A<π,0<C<π,∴A+C=π,
∴B+D=π,∴cosB=-cosD,
由余弦定理可得AC2=AB2+BC2-2AB•BCcosB=40-24cosB;
同理可AC2=AD2+CD2-2AD•CDcosD=20+16cosB;
联立以上两式可得cosB=$\frac{1}{2}$,∴sinB=$\frac{\sqrt{3}}{2}$,
∴四边形ABCD的面积S=$\frac{1}{2}$AB•BC•sinB+$\frac{1}{2}$AD•CD•sinD=$\frac{1}{2}$×2×6×$\frac{\sqrt{3}}{2}$+$\frac{1}{2}$×4×2×$\frac{\sqrt{3}}{2}$=$5\sqrt{3}$,
故答案为:5$\sqrt{3}$
点评 本题考查平面向量的数量积和解三角形,涉及三角形的面积公式余弦定理,属中档题.

 53随堂测系列答案
53随堂测系列答案| A. | $\sqrt{3}$x+y-7=0 | B. | $\sqrt{3}$x-y+7=0 | C. | x+$\sqrt{3}$y-7=0 | D. | x-$\sqrt{3}$y-7=0 |
| A. | 向左平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
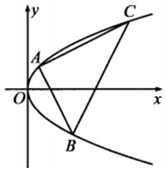 已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.