题目内容
等比数列{an}中,已知a2=4,a5=32.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若a3,a5分别为等差数列{bn}的第3项和第5项,试求数列{bn}的通项公式及前n项和Sn.
考点:等差数列的性质,等差数列的前n项和
专题:等差数列与等比数列
分析:(1)设等比数列{an}的公比为q,可得q3=
,可得q可得通项公式;(2)由(1)知a3=8,a5=32,可得b3=8,b5=32,可得等差数列{bn}的公差,进而可得通项公式和求和公式.
| a5 |
| a2 |
解答:
解:(1)设等比数列{an}的公比为q,
则q3=
=
=8,解得q=2
∴an=a2qn-2=4×2n-2=2n;
(2)由(1)知a3=8,a5=32,
∴b3=8,b5=32,
∴等差数列{bn}的公差d=
=
=12,
∴bn=b3+(n-3)d=8+12(n-3)=12n-28,
∴b1=12-28=-16,
∴Sn=nb1+
d=-16n+
×12=6n2-22n
则q3=
| a5 |
| a2 |
| 32 |
| 4 |
∴an=a2qn-2=4×2n-2=2n;
(2)由(1)知a3=8,a5=32,
∴b3=8,b5=32,
∴等差数列{bn}的公差d=
| b5-b3 |
| 5-3 |
| 32-8 |
| 2 |
∴bn=b3+(n-3)d=8+12(n-3)=12n-28,
∴b1=12-28=-16,
∴Sn=nb1+
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
点评:本题考查等差数列和等比数列的性质和通项公式,属中档题.

练习册系列答案
相关题目
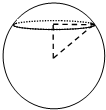 用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是
用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是