题目内容
求下列函数的值域:
(1)y=3cos(2x+
),(-
≤x≤
)
(2)y=-2sin(x+
),(-
≤x≤
)
(3)y=cos2x-2cosx+3,(x∈R)
(4)y=sin2x-cosx+1,(x∈R)
(1)y=3cos(2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
(2)y=-2sin(x+
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
(3)y=cos2x-2cosx+3,(x∈R)
(4)y=sin2x-cosx+1,(x∈R)
考点:三角函数的最值
专题:三角函数的求值
分析:(1)由x得范围得到2x+
的范围,则函数值域可求;
(2)由x得范围得到x+
的范围,则函数值域可求;
(3)函数为关于cosx的二次函数,由-1≤cosx≤1利用配方法求得函数值域;
(4)化正弦为余弦,然后由-1≤cosx≤1利用配方法求得函数值域.
| π |
| 3 |
(2)由x得范围得到x+
| π |
| 3 |
(3)函数为关于cosx的二次函数,由-1≤cosx≤1利用配方法求得函数值域;
(4)化正弦为余弦,然后由-1≤cosx≤1利用配方法求得函数值域.
解答:
解:(1)∵(-
≤x≤
),∴2x+
∈[0,
],
则y=3cos(2x+
)的值域为[-
,1];
(2)∵-
≤x≤
,∴x+
∈[-
,
],
则y=-2sin(x+
)的值域为[-2,1];
(3)y=cos2x-2cosx+3=(cosx-1)2+2,
∵-1≤cosx≤1,∴y∈[2,6];
(4)y=sin2x-cosx+1=-cos2x-cosx+2
=-(cosx+
)2+
,
∵-1≤cosx≤1,∴y∈[0,
].
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
则y=3cos(2x+
| π |
| 3 |
| 1 |
| 2 |
(2)∵-
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
则y=-2sin(x+
| π |
| 3 |
(3)y=cos2x-2cosx+3=(cosx-1)2+2,
∵-1≤cosx≤1,∴y∈[2,6];
(4)y=sin2x-cosx+1=-cos2x-cosx+2
=-(cosx+
| 1 |
| 2 |
| 9 |
| 4 |
∵-1≤cosx≤1,∴y∈[0,
| 9 |
| 4 |
点评:本题考查了三角函数最值的求法,考查了二次函数值域的求法,是基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
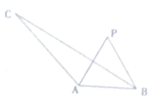 如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.
如图所示,在△ABC中,∠BAC=120°,AC=3,AB=1,P为∠BAC平分线上异于A的一点,∠APB=α,三角形PAB的面积记为S.(1)求BC的长;
(2)若α∈[
| π |
| 6 |
| π |
| 3 |
已知角α的终边过点P(-8m,-6sin30°),且cosα=-
,则m的值为( )
| 4 |
| 5 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
定义一种新运算:a?b=
,已知函数f(x)=(1+
)?log
x,若函数g(x)=f(x)-k恰有两个零点,则k的取值范围为( )
|
| 2 |
| x |
| 2 |
| A、(1,2] |
| B、(1,2) |
| C、(0,2) |
| D、(0,1) |
函数f(x)=x2+4x+5的单调递增区间是( )
| A、(-∞,-2] |
| B、[-2,+∞) |
| C、[-5,-2] |
| D、[-2,1] |
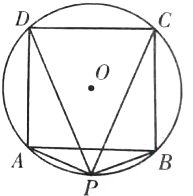 如图,设四边形ACBD是⊙O的内接正方形,P是⊙O上的任一点,求证:|
如图,设四边形ACBD是⊙O的内接正方形,P是⊙O上的任一点,求证:|