题目内容
△ABC中,三内角A,B,C分别对三边a,b,c,已知a=1,当时cosA+2cos
取最大值时,△ABC面积的最大值是 .
| B+C |
| 2 |
考点:三角函数中的恒等变换应用
专题:解三角形
分析:由诱导公式和二次函数的最值易得A=60°时,原式取到最大值,由余弦定理和三角形的面积公式以及基本不等式可得.
解答:
解:由题意可得cosA+2cos
=cosA+2cos(
)
=cosA+2sin
=-2sin2
+2sin
+1,
由二次函数可知当sin
=
即A=60°时,上式取到最大值,
由余弦定理可得1=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
∴bc≤1,当且仅当b=c=1时取等号,
∴△ABC面积S=
bcsinA=
bc≤
故答案为:
| B+C |
| 2 |
| π-A |
| 2 |
=cosA+2sin
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
由二次函数可知当sin
| A |
| 2 |
| 1 |
| 2 |
由余弦定理可得1=b2+c2-2bccosA=b2+c2-bc≥2bc-bc=bc,
∴bc≤1,当且仅当b=c=1时取等号,
∴△ABC面积S=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查三角形的面积公式和余弦定理,涉及二次函数的最值和三角函数公式的应用以及基本不等式,属中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 如图,半径都为1的三个圆两两相交,
如图,半径都为1的三个圆两两相交, |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知:α,β是不同的平面,l,m,n是不同的直线,则下列说法正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
| cos200 |
| sin200 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
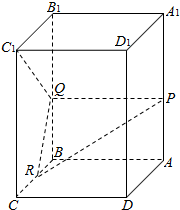 已知正四棱柱ABCD-A1B1C1D1,底面边长为
已知正四棱柱ABCD-A1B1C1D1,底面边长为