题目内容
 将全体正奇数排成一个三角形数阵(如图):按照以上排列的规律,第n行(n≥3)从左向右的第2个数为
将全体正奇数排成一个三角形数阵(如图):按照以上排列的规律,第n行(n≥3)从左向右的第2个数为考点:归纳推理
专题:计算题,推理和证明
分析:根据数阵的排列规律确定第n行(n≥3)从左向右的第2个数为多少个奇数即可.
解答:
解:根据三角形数阵可知,第n行奇数的个数为n个,则前n-1行奇数的总个数为1+2+3+…+(n-1)=
个,
则第n行(n≥3)从左向右的第2个数为第
+2个奇数,
所以此时第2个数为:2[
+2-1]+1=n2-n+3.
故答案为:n2-n+3.
| n(n-1) |
| 2 |
则第n行(n≥3)从左向右的第2个数为第
| n(n-1) |
| 2 |
所以此时第2个数为:2[
| n(n-1) |
| 2 |
故答案为:n2-n+3.
点评:本题主要考查归纳推理的应用,利用等差数列的通项公式是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线y=x3与直线y=x所围成图形的面积为( )
A、
| ||
B、
| ||
C、2
| ||
D、2
|
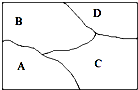 如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有
如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有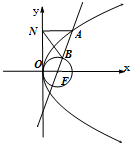 如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
如图,抛物线C:y2=2px(p>0)的焦点为F,A为C上的点,以F为圆心,
