Question

曲线y=x³与直线y=x所围成图形的面积为（　　）

• A、

  ∫

  1 -1

  (x-x3)dx
• B、

  ∫

  1 -1

  (x3-x)dx
• C、2

  ∫

  1 0

  (x-x3)dx
• D、2

  ∫

  1 0

  (x3-x)dx

Answer 1

考点：定积分在求面积中的应用

专题：导数的综合应用

分析：先求出曲线y=x³与y=x的交点坐标，得到积分的上下限，然后利用定积分求出第一象限所围成的图形的面积，根据图象的对称性可求出第三象限的面积，从而求出所求．

解答： 解：曲线y=x³与y=x的交点坐标为（0，0），（1，1），（-1，-1）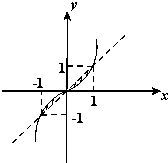
曲线y=x³与直线y=x在第一象限所围成的图形的面积是

∫

1 0

(x-x3)dx，
根据y=x³与y=x都是奇函数，关于原点对称，在第三象限的面积与第一象限的面积相等
∴曲线y=x³与y=x所围成的图形的面积为2

∫

1 0

(x-x3)dx，
故选C．

点评：本小题考查根据定积分的几何意义，以及会利用定积分求图形面积的能力，同时考查了函数图象的对称性．