题目内容
 我们把离心率e=
我们把离心率e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac,则该双曲线是黄金双曲线;
③若F1,F2为左右焦点,A1,A2为左右顶点,B1(0,b),B2(0,-b)且∠F1B1A2=90°,则该双曲线是黄金双曲线;
④若MN经过右焦点F2且MN⊥F1F2,∠MON=90°,则该双曲线是黄金双曲线.
其中正确命题的序号为
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:利用双曲线的简单性质分别求出离心率,再利用黄金双曲线的定义求解.
解答:
解:①双曲线x2-
=1中,
∵e=
=
,
∴双曲线x2-
=1是黄金双曲线,故①正确;
②b2=ac,则e=
=
=
,
∴e2-e-1=0,解得e=
,或e=
(舍),
∴该双曲线是黄金双曲线,故②正确;
③如图,F1,F2为左右焦点,A1,A2为左右顶点,
B1(0,b),B2(0,-b),且∠F1B1A2=90°,
∴B1F12+B1A22=A2F12,即b2+2c2=(a+c)2,
整理,得b2=ac,由②知该双曲线是黄金双曲线,故③正确;
④如图,MN经过右焦点F2且MN⊥F1F2,∠MON=90°,
∴NF2=OF2,∴
=c,∴b2=ac,
由②知该双曲线是黄金双曲线,故④正确.
故答案为:①②③④.
| 2y2 | ||
|

∵e=
| ||||||
| 1 |
| ||
| 2 |
∴双曲线x2-
| 2y2 | ||
|
②b2=ac,则e=
| c |
| a |
| ||
| a |
| 1+e |
∴e2-e-1=0,解得e=
| ||
| 2 |
1-
| ||
| 2 |
∴该双曲线是黄金双曲线,故②正确;
③如图,F1,F2为左右焦点,A1,A2为左右顶点,
B1(0,b),B2(0,-b),且∠F1B1A2=90°,
∴B1F12+B1A22=A2F12,即b2+2c2=(a+c)2,
整理,得b2=ac,由②知该双曲线是黄金双曲线,故③正确;
④如图,MN经过右焦点F2且MN⊥F1F2,∠MON=90°,
∴NF2=OF2,∴
| b2 |
| a |
由②知该双曲线是黄金双曲线,故④正确.
故答案为:①②③④.
点评:本题考查黄金双曲线的判断,是中档题,解题时要认真审题,注意双曲线的性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式(x-1)(x-2)<0的解集是( )
| A、(1,2) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(-∞,-2)∪(-1,+∞) |
设D={(x+y)|
},若P∈D,有且只有一条直线OP(O为坐标原点),使得该直线与曲线f(x)=
asinx在原点处相切,则a的取值范围是( )
|
| 1 |
| 2 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
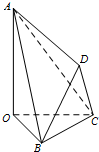 如图,四面体OABC中,OA,OB,OC两两垂直,且OA=
如图,四面体OABC中,OA,OB,OC两两垂直,且OA=