题目内容
如图是一个几何体的三视图，根据图中数据：（Ⅰ）计算该几何体的表面积（两个几何体的连接点忽略不计）；
（Ⅱ）计算该几何体的体积．
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图可知，该几何体是上面为球体下面为圆柱的组合体，直接求表面积、条件体积即可．
解答：
解：该几何体是上面为球体下面为圆柱的组合体
（Ⅰ）计算该几何体的表面积（两个几何体的连接点忽略不计）；
由已知球半径为r=1，则圆柱底面圆半径为r=1，圆柱高h=3
S=4π×1+2π×1+2π×1×3=12π．-----------------------------------------（4分）
（Ⅱ）该几何体的体积V=
π×1+π×1×3=
．----------------（8分）
（Ⅰ）计算该几何体的表面积（两个几何体的连接点忽略不计）；
由已知球半径为r=1，则圆柱底面圆半径为r=1，圆柱高h=3
S=4π×1+2π×1+2π×1×3=12π．-----------------------------------------（4分）
（Ⅱ）该几何体的体积V=
| 4 |
| 3 |
| 13π |
| 3 |
点评：本题考查三视图、组合体的表面积、体积．考查简单几何体的三视图的运用；培养同学们的空间想象能力和基本的运算能力；中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
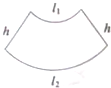如图是一个扇环（圆环的一部分），两段圆弧的长分别为l1，l2，另外两边的长为h，先把这个扇环与梯形类比，然后根据梯形的面积公式写出这个扇环的面积并证明其正确性．参考公式：
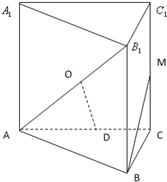已知直三棱柱ABC-A1B1C1的底面△ABC中，∠C=90°，BC=
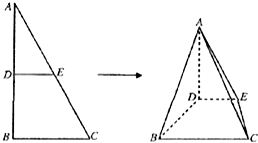如图，△ABC中，AB=2，BC=1，∠ABC=90°，D，E分别为AB，AC上的点，DE∥BC，将△ADE沿DE折到△A′DE的位置，使平面A′DE⊥平面BCED．