题目内容
若函数f(x)=|2x-m|的单调递增区间是[2,+∞),则m= .
考点:函数单调性的性质,利用导数研究函数的单调性
专题:函数的性质及应用
分析:根据绝对值函数的性质即可得到结论.
解答:
解:f(x)=|2x-m|=
,
即当x≥
时,函数f(x)单调递增,
若函数f(x)=|2x-m|的单调递增区间是[2,+∞),
则
=2,即m=4,
故答案为:4.
|
即当x≥
| m |
| 2 |
若函数f(x)=|2x-m|的单调递增区间是[2,+∞),
则
| m |
| 2 |
故答案为:4.
点评:本题主要考查函数单调性的应用,要求根据绝对值函数的性质是解决本题的关键.

练习册系列答案
相关题目
已知中心在原点的椭圆C的右焦点为F(3,0),离心率等于
,则椭圆的方程是( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
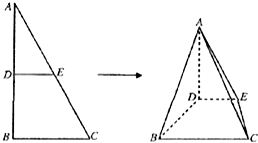 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.