题目内容
设数列{an}满足an+1+an-1=2an(n≥2),Sn是数列{an}的前n项和,S9=99,a10=21.
(1)求数列{an}的前n项和Sn;
(2)设Tn=
+
+…+
,求Tn.
(1)求数列{an}的前n项和Sn;
(2)设Tn=
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得数列{an}是等差数列,由解得a1=3,d=2,由此能求出Sn=n2+2n.
(3)由
=
=
(
-
),利用裂项求和法能求出Tn.
(3)由
| 1 |
| Sn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
解答:
解:(1)∵数列{an}满足an+1+an-1=2an(n≥2),
∴数列{an}是等差数列,
∵S9=99,a10=21,
∴
,解得a1=3,d=2,
∴Sn=3n+
×2=n2+2n.
(3)
=
=
(
-
),
∴Tn=
+
+…+
=
(1-
+
-
+
-
+…+
-
)
=
(1+
-
-
)
=
(
-
-
).
∴数列{an}是等差数列,
∵S9=99,a10=21,
∴
|
∴Sn=3n+
| n(n-1) |
| 2 |
(3)
| 1 |
| Sn |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴Tn=
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| n |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质和裂项求和法的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
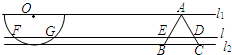 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧