题目内容
已知a+b＞0，用分析法证明：
≥
（a+b）．
| a2+b2 |
| ||
| 2 |
考点：综合法与分析法(选修）
专题：不等式
分析：本题指定用分析法证明，通过分析得到易证命题，从而证得原命题成立．
解答：
证明：要证：
≥
（a+b），
只要证：a2+b2≥
(a+b)2，
只要证：2a2+2b2≥a2+2ab+b2，
只要证：a2-2ab+b2≥0，
只要证：（a-b）2≥0．
∵a+b＞0，
∴（a-b）2≥0．
∴原命题成立．
| a2+b2 |
| ||
| 2 |
只要证：a2+b2≥
| 1 |
| 2 |
只要证：2a2+2b2≥a2+2ab+b2，
只要证：a2-2ab+b2≥0，
只要证：（a-b）2≥0．
∵a+b＞0，
∴（a-b）2≥0．
∴原命题成立．
点评：本题考查的是用分析法证明不等式，本题难度不大，属于基础题．
练习册系列答案
相关题目
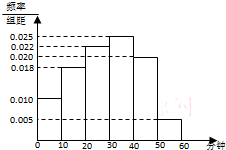电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查．如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图； 将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”