题目内容
在△ABC中,cos(A-C)+2cos2
=
,三边a,b,c成等比数列,求B.
| B |
| 2 |
| 5 |
| 2 |
由已知得:cos(A-C)+cosB=
,
cos(A-C)+cos(A+C)=
,
∴sinAsinC=
,
又∵a,b,c成等比数列,∴b2=ac,
又由正弦定理得sin2B=sinA•sinC,
∴sin2B=
,sinB=
,(-
舍去),
∴B=60°或120°,
但若B=120°,则有b>a,b>c,b2>ac,
这与已知b2=ac矛盾,故B≠120°,
∴B=60°
| 3 |
| 2 |
cos(A-C)+cos(A+C)=
| 3 |
| 2 |
∴sinAsinC=
| 3 |
| 4 |
又∵a,b,c成等比数列,∴b2=ac,
又由正弦定理得sin2B=sinA•sinC,
∴sin2B=
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
∴B=60°或120°,
但若B=120°,则有b>a,b>c,b2>ac,
这与已知b2=ac矛盾,故B≠120°,
∴B=60°

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
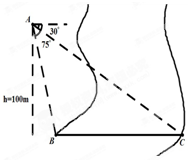
 中,若
中,若 ,则
,则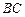 等于 ( )
等于 ( )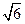 B
B C
C  D
D 