题目内容

在平面直角坐标系xOy中，已知三角形ABC顶点A和C是椭圆
x2
25
+
y2
16
=1的两个焦点，顶点B在椭圆
x2
25
+
y2
16
=1上，则
sinA+sinC
sinB
=______．
根据题意，可得椭圆
x2
25
+
y2
16
=1中，a=5，b=4．
所以c=
a2-b2
=3，可得焦点坐标为A（-3，0），C（3，0）．
∵△ABC的顶点A和C是椭圆
x2
25
+
y2
16
=1的两个焦点，顶点B在椭圆
x2
25
+
y2
16
=1上
∴根据正弦定理，可知
sinA+sinC
sinB
=
|AB|+|BC|
|AC|
=
2a
2c
=
5
3
．
故答案为：
5
3
练习册系列答案
相关题目
已知函数的图像过点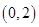，且函数图像的两相邻对称轴间的距离为.
（1）当时，求函数的值域；
（2）设，求函数的单调区间.
在△ABC中，角A、B、C的对边分别为a，b，c，已知（b+c）：（c+a）：（a+b）=4：5：6，则下列结论正确的是______
（1）△ABC一定是钝角三角形；
（2）△ABC被唯一确定；
（3）sinA：sinB：sinC=7：5：3；
（4）若b+c=8，则△ABC的面积为
15
3
2
．
在△ABC中，cos(A-C)+2cos2
B
2
=
5
2
，三边a，b，c成等比数列，求B．
在△ABC中，角A、B、C所对的边分别为a、b、c，且f（A）=2cos
A
2
sin（π-
A
2
）+sin2
A
2
-cos2
A
2
．
（Ⅰ）求函数f（A）的最大值；
（Ⅱ）若f（A）=0，C=
5π
12
，a=
6
，求b的值．
在△ABC中，角A，B，C的对边分别为a，b，c，若a2+b2=4a+2b-5，且a2=b2+c2-bc，则sinB的值为______．
设△ABC的内角A、B、C所对边分别是a、b、c，已知B=60°，
（1）若b=
3
，A=45°，求a；
（2）若a、b、c成等比数列，请判断△ABC的形状．
已知角A，B，C是△ABC的内角，a，b，c分别是其对边长，向量
m
=(2
3
sin
A
2
，cos2
A
2
)，
n
=(cos
A
2
，-2)，
m
⊥
n
．
（1）求角A的大小；
（2）若a=2，cosB=
3
3
，求b的长．
在△ABC中，a，b，c分别是BC，AC，AB三边的长，已知a=8，B=60°，C=75°，则b等于______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网