题目内容
已知a，b，c∈R+，a+b+c=
，求证：a2+b2+c2≥1．
| 3 |
考点：不等式的证明
专题：证明题,不等式的解法及应用
分析：利用基本不等式、以及不等式的性质，证得要证的不等式．
解答：
证明：依题意得：（a+b+c）2=a2+b2+c2+2ab+2bc+2ac≤a2+b2+c2+（a2+b2）+（b2+c2）+（a2+c2）
=3（a2+b2+c2）．
∵a+b+c=
，
∴a2+b2+c2≥1．
=3（a2+b2+c2）．
∵a+b+c=
| 3 |
∴a2+b2+c2≥1．
点评：本题主要考查利用基本不等式、不等式的性质，利用综合法证明不等式，属于中档题．
练习册系列答案
相关题目
已知椭圆C的上、下顶点分别为B1、B2，左、右焦点分别为F1、F2，若四边形B1F1B2F2是正方形，则此椭圆的离心率e等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
在第二象限内单调递增，则m的最大负整数是（ ）
| 1 |
| x1-m |
| A、-4 | B、-3 | C、-2 | D、-1 |
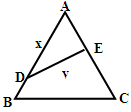如图，公园有一块边长为2的等边的三角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．设AD=x（x≥0），DE=y，求用x表示y的函数关系式，并求函数的定义域．
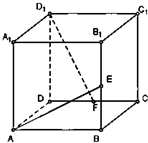如图，在正方体ABCD-A1B1C1D1中，E、F分别是BB1、DC的中点．