题目内容
已知椭圆C的上、下顶点分别为B1、B2,左、右焦点分别为F1、F2,若四边形B1F1B2F2是正方形,则此椭圆的离心率e等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据已知条件知b=c,所以a=
=
=
c,这样即可求出离心率e=
.
| b2+c2 |
| c2+c2 |
| 2 |
| c |
| a |
解答:
解:由已知条件知:b=c,∴a=
=
c;
∴椭圆的离心率为
=
=
.
故选C.
| c2+c2 |
| 2 |
∴椭圆的离心率为
| c |
| a |
| c | ||
|
| ||
| 2 |
故选C.
点评:考查椭圆的几何性质,椭圆的离心率及离心率公式.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
 若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )
若某三棱柱截去一个三棱锥后所剩几何体的三视图如图所示,则此几何体的体积等于( )| A、30 | B、12 | C、24 | D、4 |
下列集合中为空集的是( )
| A、{x∈N|x2≤0} |
| B、{x∈R|x2-1=0} |
| C、{x∈R|x2+x+1=0} |
| D、{0} |
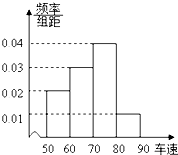 某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )
某雷达测速区规定:凡车速大于或等于80km/h的汽车视为“超速”,并将受到处罚.如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则从图中可以看出被处罚的汽车大约有( )| A、20辆 | B、40辆 |
| C、60辆 | D、80辆 |
若集合M={y|y=3x},集合S={x|y=lg(x-1)},则下列各式正确的是( )
| A、M∪S=M | B、M∪S=S |
| C、M=S | D、M∩S=∅ |