题目内容
设函数y=f(x)的定义域为R,若对于给定的正数k,定义函数fk(x)=
则当函数f(x)=
,k=1时,定积分
fk(x)dx的值为 .
|
| 1 |
| x |
| ∫ | 2
|
考点:定积分
专题:导数的综合应用
分析:根据fk(x)的定义求出fk(x)的表达式,然后根据积分的运算法则即可得到结论.
解答:
解:由定义可知当k=1时,f1(x)=
,即f1(x)=
,
则定积分
fk(x)dx=
dx+
1dx=lnx|
+x|
=ln1-ln
+2-1=1+2ln2,
故答案为:1+2ln2.
|
|
则定积分
| ∫ | 2
|
| ∫ | 1
|
| 1 |
| x |
| ∫ | 2 1 |
1
|
2 1 |
| 1 |
| 4 |
故答案为:1+2ln2.
点评:本题主要考查积分的计算,利用函数的定义求出函数的表达式是解决本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
球面上有M、N两点,在过M、N的球的大圆上,
的度数为90°,在过M、N的球小圆上,
的度数为120°,又MN=
cm,则球心到上述球小圆的距离是( )
 |
| MN |
 |
| MN |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1cm |
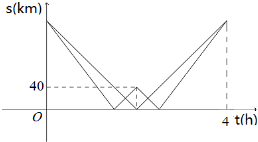 A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行
A,B两架直升机同时从机场出发,完成某项救灾物资空投任务.A机到达甲地完成任务后原路返回;B机路过甲地,前往乙地完成任务后原路返回.如图中折线分别表示A,B两架直升机离甲地的距离s与时间t之间的函数关系.假设执行任务过程中A,B均匀速直线飞行,则B机每小时比A机多飞行