题目内容
14.已知cos(α+β)cosα+sin(α+β)sinα=$\frac{1}{3}$,β∈($\frac{3π}{2}$,2π),求cos(β-$\frac{π}{4}$)的值.分析 由已知及两角差的余弦函数公式可求cosβ=$\frac{1}{3}$,结合范围β∈($\frac{3π}{2}$,2π),利用同角三角函数基本关系式可求sinβ,由特殊角的三角函数值及两角差的余弦函数公式即可求值.
解答 解:∵cos(α+β)cosα+sin(α+β)sinα=cos[(α+β)-α]=cosβ=$\frac{1}{3}$,
∵β∈($\frac{3π}{2}$,2π),
∴sinβ=-$\sqrt{1-co{s}^{2}β}$=-$\frac{2\sqrt{2}}{3}$,
∴cos(β-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$(cosβ+sinβ)=$\frac{\sqrt{2}}{2}$×($\frac{1}{3}-\frac{2\sqrt{2}}{3}$)=$\frac{\sqrt{2}-4}{6}$.
点评 本题主要考查了两角差的余弦函数公式,同角三角函数基本关系式,特殊角的三角函数值等知识在三角函数求值中的综合应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
5.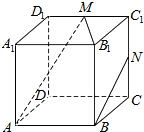 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为( )
 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为( )
| A. | ③④ | B. | ①② | C. | ①③ | D. | ②④ |
2.下列积分均存在,则下列结论错误的是( )
| A. | d(∫f(x)dx)=f(x)dx | B. | ∫f(x)dx=∫f(u)du | ||
| C. | ${∫}_{a}^{b}$f(x)dx=${∫}_{a}^{b}$f(u)du | D. | ${∫}_{a}^{b}$f(x)dx+${∫}_{b}^{a}$f(x)dx=0. |