题目内容
3.已知圆${O_1}:{x^2}+{y^2}=1$与圆${O_{2:}}{({x-3})^2}+{({y+4})^2}=16$,则两圆的位置关系为( )| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
分析 计算两圆的圆心距和半径,根据他们的大小关系得出结论.
解答 解:圆O1的圆心为(0,0),半径为r=1,
圆O2的圆心为(3,-4),半径为R=4,
∴两圆的圆心距d=$\sqrt{9+16}$=5,
∴d=R+r,
故两圆外切.
故选:C.
点评 本题考查了圆的位置关系判断,属于基础题.

练习册系列答案
相关题目
12.已知二面角α-AB-β的平面角是锐角θ,α内一点C到β的距离为3,点C到棱AB的距离为4,那么cosθ的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{{3\sqrt{7}}}{7}$ | D. | $\frac{\sqrt{7}}{4}$ |
10.定义在实数域上的偶函数f(x)对于?x∈R,均满足条件f(x+2)=f(x)+f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上恰有4个零点,则a的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
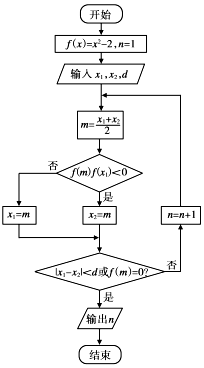 二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( )
二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入x1=1,x2=2,d=0.01则输出n的值( ) 与直线
与直线 间的距离是 .
间的距离是 .