题目内容
10.定义在实数域上的偶函数f(x)对于?x∈R,均满足条件f(x+2)=f(x)+f(1),且当x∈[2,3]时,f(x)=-2x2+12x-18,若函数y=f(x)-loga(|x|+1)在(0,+∞)上恰有4个零点,则a的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{6}}{6}$ |
分析 利用f(x)的奇偶性判断f(x)的周期,作出f(x)和y=loga(x+1)在(0,+∞)上的函数图象,根据交点个数判断y=loga(x+1)的特殊点位置.
解答 解:令x=-1得f(1)=f(-1)+f(1)=2f(1),
∴f(1)=0,∴f(x+2)=f(x),
∴f(x)的周期为2.
作出f(x)的函数图象如图所示:
∵y=f(x)-loga(|x|+1)在(0,+∞)上恰有4个零点,
∴loga5=-2,解得a=$\frac{\sqrt{5}}{5}$.
故选C.
点评 本题考查了函数零点与函数图象的关系,函数周期与奇偶性的应用,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
5.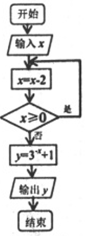 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )
 根据如图,当输入x为2017时,输出的y为( )
根据如图,当输入x为2017时,输出的y为( )| A. | $\frac{4}{3}$ | B. | 10 | C. | 4 | D. | 2 |
18.函数f(x)=$\left\{\begin{array}{l}{0,x∈\{0,4\}}\\{{x}^{2}-2x+3,0<x≤2}\\{|x-3|,2<x<4}\end{array}\right.$,若f(x)=kx有三个不同的根,则实数k的取值范围是( )
| A. | (0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | B. | [0,$\frac{1}{4}$)∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | C. | [0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] | D. | (0,$\frac{1}{4}$]∪(2$\sqrt{3}$-2,$\frac{3}{2}$] |
5.春节期间和谐小区从初一至初八连续8天举办大型文艺汇演,居民甲随机选择其中的连续3天观看演出,那么他在初一至初四期间连续3天看演出的概率为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
2.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位,则z1z2=( )
| A. | 1-2i | B. | 5i | C. | -5 | D. | 5 |
16.在拍毕业照时,六个同学排成一排照相,要求其中一对好友甲和乙相邻,且同学丙不能和甲相邻的概率为( )
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $\frac{4}{15}$ | D. | $\frac{1}{5}$ |
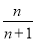 ,则
,则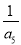 等于( )
等于( )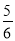 B.
B.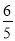 C.
C.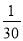 D.30
D.30