题目内容
在等腰直角△ABC中AC=BC,E为AC的中点,ED⊥AB于点D,将△ADE沿DE折起后为△A′DE使得面A′DE⊥面BCED.若F为线段A′B上一点及
=λ.
①当λ=
时,求证:FC∥面A′DE;
②当二面角∠B-DF-C的余弦值为值
,求λ的值.
| A′F |
| A′B |
①当λ=
| 1 |
| 3 |
②当二面角∠B-DF-C的余弦值为值
| 3 |
| 7 |
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:①设等腰直角△ABC中,AC=BC=2,以D为原点,DB为x轴,DE为y轴,DA′为z轴,建立空间直角坐标系,由向量法求出
=(0,-
,
)和平面A′DE的法向量
=(1,0,0),由此能证明CF∥平面A′DE.
②分别求出平面BDF的法向量和平面CDF的法向量,由此利用向量法能求出二面角∠B-DF-C的余弦值
时λ=
.
| CF |
| 2 |
| ||
| 3 |
| m |
②分别求出平面BDF的法向量和平面CDF的法向量,由此利用向量法能求出二面角∠B-DF-C的余弦值
| 3 |
| 7 |
| 1 |
| 10 |
解答:
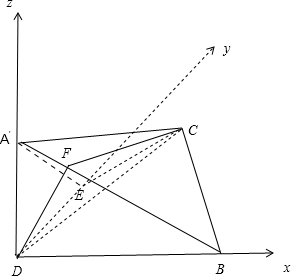 ①证明:设等腰直角△ABC中,AC=BC=2,
①证明:设等腰直角△ABC中,AC=BC=2,
则AB=
=2
,C到AB的距离d=
,DE=AD
,
如图,以D为原点,DB为x轴,DE为y轴,
DA′为z轴,建立空间直角坐标系,
A′(0,0,
,B(
,0,0),设F(a,b,c),
∵
=λ,λ=
,∴
=
,
∴(a,b,c-
)=(
,0,-
),
∴a=
,b=0,c=
,∴F(
,0,
),
∵C(
,
,0),∴
=(0,-
,
),
∵平面A′DE的法向量
=(1,0,0),
∴
•
=0,又CF?平面A′DE,
∴CF∥平面A′DE.
②由已知得平面BDF的法向量
=(0,1,0),
D(0,0,0),C(
,
,0),A′(0,0,
,B(
,0,0),设F(a,b,c),
=(a,b,c-
),
=(
,0,-
),
=(
,
,0),
∵
=λ,∴
=λ
,∴
,∴
=(
λ,0,
-
λ),
设平面CDF的法向量
=(x1,y1,z1),
则
,取x1=2,得
=(2,-1,
),
∵二面角∠B-DF-C的余弦值
,
∴|cos<
,
>|=|
|=
=
,
由0≤λ≤1,解得λ=
.
 ①证明:设等腰直角△ABC中,AC=BC=2,
①证明:设等腰直角△ABC中,AC=BC=2,则AB=
| 4+4 |
| 2 |
| 2 |
| ||
| 2 |
如图,以D为原点,DB为x轴,DE为y轴,
DA′为z轴,建立空间直角坐标系,
A′(0,0,
| ||
| 2 |
3
| ||
| 2 |
∵
| A′F |
| A′B |
| 1 |
| 3 |
| A′F |
| 1 |
| 3 |
| A′B |
∴(a,b,c-
| ||
| 2 |
| ||
| 2 |
| ||
| 6 |
∴a=
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
∵C(
| ||
| 2 |
| 2 |
| CF |
| 2 |
| ||
| 3 |
∵平面A′DE的法向量
| m |
∴
| m |
| CF |
∴CF∥平面A′DE.
②由已知得平面BDF的法向量
| n |
D(0,0,0),C(
| ||
| 2 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| A′F |
| ||
| 2 |
| A′B |
3
| ||
| 2 |
| ||
| 2 |
| DC |
| ||
| 2 |
| 2 |
∵
| A′F |
| A′B |
| A′F |
| A′B |
|
| DF |
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
设平面CDF的法向量
| p |
则
|
| p |
| 6λ |
| λ-1 |
∵二面角∠B-DF-C的余弦值
| 3 |
| 7 |
∴|cos<
| n |
| p |
| -1 | ||||
|
| 1 | ||||
|
| 3 |
| 7 |
由0≤λ≤1,解得λ=
| 1 |
| 10 |
点评:本题考查直线与平面平行的证明,考查满足条件的实数值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
设
,
是两个空间向量,若|
|=1,
=(0,2,1),
=λ
(λ∈R),则λ=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、
|
已知函数y=ax的反函数是f(x)且f(
)=
,则a=( )
| 2 |
| 1 |
| 2 |
| A、4 | ||
B、
| ||
C、
| ||
| D、2 |
设a∈R,集合A={x|(x-1)(x-a)≥0},B={(a-1)x≥a2-2a+1},若A∪B=R,则a的取值范围为( )
| A、(-∞,2) |
| B、(2,+∞) |
| C、(1,2] |
| D、(1,2) |
设a>0,b>0,若
是5a与5b的等比中项,则
+
的最小值为( )
| 5 |
| 2 |
| a |
| 1 |
| b |
| A、6 | ||
B、3+2
| ||
| C、1 | ||
D、
|
设α为锐角,若cos(α+
)=
,则sin(2α+
)的值为( )
| π |
| 6 |
| 4 |
| 5 |
| π |
| 12 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.
某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示.