题目内容
11.已知复数z的共轭复数$\overline{z}$,且$\overline{z}=\frac{z}{1+i}$+2(i为虚数单位),则z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 设复数z=a+bi,a,b∈R,i为虚数单位,利用复数相等列出方程组求出a、b的值,即可判定z在复平面内对应的点位于第几象限.
解答 解:设复数z=a+bi,a,b∈R,i为虚数单位,
则z的共轭复数为$\overline{z}$=a-bi;
又$\overline{z}=\frac{z}{1+i}$+2,
∴a-bi=$\frac{a+bi}{1+i}$+2,
即a-bi=$\frac{(a+bi)(1-i)}{1{-i}^{2}}$+2,
∴a-bi=($\frac{a+b}{2}$+2)-$\frac{a-b}{2}$i,
∴$\left\{\begin{array}{l}{a=\frac{a+b}{2}+2}\\{b=\frac{a-b}{2}}\end{array}\right.$,
解得a=6,b=2,
∴z=6+2i;
∴z在复平面内对应的点位于第一象限.
故选:A.
点评 本题考查了复数的定义与应用问题,也考查了方程组的解法与应用问题,是基础题目.

练习册系列答案
相关题目
2.设a=tan$\frac{π}{7}$,b=$\frac{π}{7}$,c=sin$\frac{π}{7}$,则a,b,c的大小关系是( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
19.已知a=(1-i)(1+bi),其中a,b是实数,i是虚数单位,则$\frac{a+bi}{i}$=( )
| A. | 2+i | B. | 1+2i | C. | 2-i | D. | 1-2i |
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1(-c,0)、F2(c,0),P是椭圆C上一点,且|PF2|=|F1F2|,直线PF1与圆x2+y2=$\frac{{c}^{2}}{4}$相切,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
 有两个不相等的实数根,则
有两个不相等的实数根,则 的值可以是 (写出一个即可).
的值可以是 (写出一个即可). 分别是定义在
分别是定义在 上的奇函数和偶函数,且
上的奇函数和偶函数,且 ,若存在
,若存在 ,使得等式
,使得等式 成立,则实数
成立,则实数 的取值范围是 .
的取值范围是 . ,二次函数
,二次函数 ,关于
,关于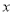 的不等式
的不等式 的解集为
的解集为 ,其中
,其中 为非零常数,设
为非零常数,设 .
.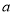 的值;
的值;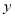 轴垂直的直线和函数
轴垂直的直线和函数 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标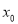 满足
满足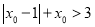 ,求实数
,求实数 的取值范围;
的取值范围;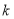 取何值时,函数
取何值时,函数 存在极值?并求出相应的极值点.
存在极值?并求出相应的极值点.