题目内容

7．若数列{an}满足：存在正整数T，对于任意正整数n都有an+T=an成立，则称数列{an}为周期数列，周期为T．已知数列{an}满足a1=m（m＞0），${a}_{n+1}=\left\{\begin{array}{l}{{a}_{n}-1，{a}_{n}＞1}\\{\frac{1}{{a}_{n}}，0＜{a}_{n}≤1}\end{array}\right.$，若a3=4，则m的所有可能取值为（　　）
A．{6，$\frac{5}{4}$}B．{6，$\frac{5}{4}$，$\frac{2}{5}$}C．{6，$\frac{5}{4}$，$\frac{1}{5}$}D．{6，$\frac{1}{5}$}

分析 对m分类讨论，利用递推关系即可得出．

解答 解：数列{an}满足a1=m（m＞0），${a}_{n+1}=\left\{\begin{array}{l}{{a}_{n}-1，{a}_{n}＞1}\\{\frac{1}{{a}_{n}}，0＜{a}_{n}≤1}\end{array}\right.$，a3=4，
①若m＞2，则a2=m-1＞1，∴a3=m-2=4，解得m=6．
②若m=2，则a2=m-1=1，∴a3=$\frac{1}{{a}_{2}}$=1≠4，舍去．
③若1＜m＜2，则a2=m-1∈（0，1），∴a3=$\frac{1}{m-1}$=4，解得m=$\frac{5}{4}$．
④若m=1，则a2=$\frac{1}{{a}_{1}}$=1，∴a3=$\frac{1}{{a}_{2}}$≠4，舍去．
⑤若0＜m＜1，则a2=$\frac{1}{{a}_{1}}$=$\frac{1}{m}$＞1，∴a3=a2-1=$\frac{1}{m}$-1=4，解得m=$\frac{1}{5}$．
综上可得：m∈$\{6，\frac{5}{4}，\frac{1}{5}\}$．
故选：C．

点评 本题考查了等比数列的通项公式、递推关系，考查了分类讨论方法、推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
20．已知点F1、F2是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，O为坐标原点，点P在双曲线C的右支上，且满足|F1F2|=2|OP|，|PF1|≥3|PF2|，则双曲线C的离心率的取值范围为（　　）
A．（1，+∞）B．[$\frac{\sqrt{10}}{2}$，+∞）C．（1，$\frac{\sqrt{10}}{2}$]D．（1，$\frac{5}{2}$]
20．抛掷两枚骰子，当至少有一枚5点或一枚6点出现时，就说这次试验成功，求在30次试验中成功次数X的均值．
15．若命题“?x∈[0，$\frac{π}{2}$]，不等式exsinx≥kx”是真命题，则实数k的取值范围是（　　）
A．（-∞，1]B．（-∞，e${\;}^{\frac{π}{2}}$]C．（1，e${\;}^{\frac{π}{2}}$）D．[e${\;}^{\frac{π}{2}}$，+∞）
2．设a=tan$\frac{π}{7}$，b=$\frac{π}{7}$，c=sin$\frac{π}{7}$，则a，b，c的大小关系是（　　）
A．c＞b＞aB．b＞c＞aC．a＞c＞bD．a＞b＞c

先化简，再求值：，其中，.
18．若函数y=$\frac{ax+1}{x-3}$的反函数是它本身，则a的值为3．
15．计算$（\frac{27}{8}）^{-\frac{1}{3}}$-cosπ-$lo{g}_{2}（{4}^{\frac{1}{3}）}$+${{C}_{9}}^{7}$=37．
16．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1（-c，0）、F2（c，0），P是椭圆C上一点，且|PF2|=|F1F2|，直线PF1与圆x2+y2=$\frac{{c}^{2}}{4}$相切，则椭圆的离心率为（　　）
A．$\frac{1}{3}$B．$\frac{\sqrt{3}-1}{2}$C．$\frac{\sqrt{2}-1}{2}$D．$\frac{\sqrt{3}}{4}$

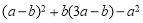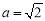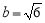违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网