题目内容
已知f(α)=
.
(1)若α=-1860°,求f(α);
(2)若cos(α-
)=
,求f(α)的值.
| sin(π+α)cos(2π-α)tan(2π-α) | ||
tan(-α-π)cos(-
|
(1)若α=-1860°,求f(α);
(2)若cos(α-
| 3π |
| 2 |
| 3 |
| 5 |
考点:两角和与差的余弦函数,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)先利用诱导公式把函数解析式化简整理,再把α=-1860°代入利用诱导公式求得答案.
(2)根据题意确定α所在的象限,进而求得sinα的,进而利用平方关系求得cosα的值、.
(2)根据题意确定α所在的象限,进而求得sinα的,进而利用平方关系求得cosα的值、.
解答:
解:f(α)=
=
=-cosα,
(1)f(-1860°)=-cos(-1860°)=-cos(360°×5π+60°)=-cos60°=-
.
(2)∵cos(α-
)=cos(
-α)=-sinα,
∴sinα=-
,且α是第三、四象限,
当α是第三象限角时,由sinα=-
,得cosα=-
,
∴f(α)=
.
当α是第三象限角时,sinα=-
,得cosα=
,
∴f(α)=-
.
| (-sinα)cosα(-tanα) | ||
-tan(π+α)cos(
|
| sinαcosαtanα |
| -tanαsinα |
(1)f(-1860°)=-cos(-1860°)=-cos(360°×5π+60°)=-cos60°=-
| 1 |
| 2 |
(2)∵cos(α-
| 3π |
| 2 |
| 3π |
| 2 |
∴sinα=-
| 3 |
| 5 |
当α是第三象限角时,由sinα=-
| 3 |
| 5 |
| 4 |
| 5 |
∴f(α)=
| 4 |
| 5 |
当α是第三象限角时,sinα=-
| 3 |
| 5 |
| 4 |
| 5 |
∴f(α)=-
| 4 |
| 5 |
点评:本题主要考查了诱导公式的应用.“一全,二正弦,三切,四余弦”是记忆象限角符号的常用方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
计算定积分
cos2xdx的值是( )
| ∫ |
|
A、
| ||||
B、
| ||||
C、
| ||||
D、2(
|
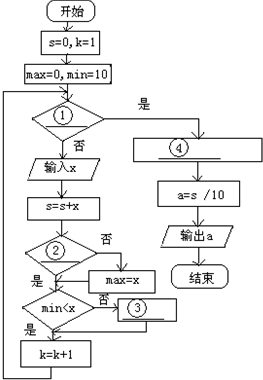 “钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).
“钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).