题目内容
已知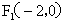 ,
,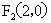 ,点
,点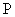 满足
满足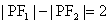 ,记点
,记点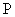 的轨迹为
的轨迹为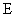 ,直线
,直线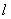 过点
过点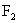 且与轨迹
且与轨迹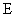 交于
交于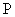 、
、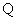 两点.
两点.
(1)无论直线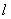 绕点
绕点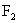 怎样转动,在
怎样转动,在 轴上总存在定点
轴上总存在定点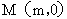 ,使
,使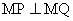 恒成立,求实数
恒成立,求实数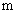 的值.
的值.
(2)过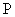 、
、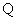 作直线
作直线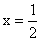 的垂线
的垂线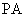 、
、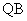 ,垂足分别为
,垂足分别为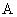 、
、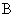 ,记
,记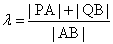 ,求
,求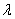 的取值范围.
的取值范围.
解:(1)由 知,点
知,点 的轨迹
的轨迹 是以
是以 、
、 为焦点的双曲线的右支,由
为焦点的双曲线的右支,由 ,
, ,∴
,∴ ,故轨迹
,故轨迹 的方程为:
的方程为:

(Ⅰ)当直线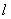 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为 ,
, ,
, ,与双曲线方程联立消
,与双曲线方程联立消 得
得 ,
,
∴
解得






 ,∴
,∴
故得 对任意的
对任意的
 恒成立,
恒成立,
∴ ,解得
,解得
∴当 时,
时,
(Ⅱ)当直线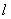 的斜率不存在时,由
的斜率不存在时,由 ,
, 及
及 知结论也成立,
知结论也成立,
综上,当 时,
时,
(2) ,
, ,∴直线
,∴直线 是双曲线的右准线,
是双曲线的右准线,
由双曲线定义得: ,
, ,
,
方法一:∴

 ,∴
,∴ ,故
,故 ,
,
注意到直线的斜率不存在时, ,此时
,此时 ,
,
 综上,
综上, .
.
方法二:设直线 的倾斜角为
的倾斜角为 ,由于直线
,由于直线 与双曲线右支有二个交点,
与双曲线右支有二个交点,
∴ ,过
,过 作
作 ,垂足为
,垂足为 ,则
,则
 ,
,
∴
由 ,得
,得 ,
,
故 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 则
则 的取值范围是 .
的取值范围是 . 是函数
是函数 的导数,要得到
的导数,要得到 的图像,只需将y=f(2x)的图像
的图像,只需将y=f(2x)的图像 个单位B向右平移
个单位B向右平移 个单位C向左平移
个单位C向左平移 个单位D向左平移
个单位D向左平移 个单位
个单位 是两个不同的平面,m,n是两条不同的直线,给出下列命题:
是两个不同的平面,m,n是两条不同的直线,给出下列命题: ;
; ;
;  相交;
相交;
 ,把数列
,把数列 的各项排列成如右侧的三角形状:
的各项排列成如右侧的三角形状:  表示第m行的第n个数,则
表示第m行的第n个数,则 ____________.
____________.  ____________。
____________。 ,
, 的焦点恰好是双曲线
的焦点恰好是双曲线 的右焦点,且两条曲线交点的连线过F,则该双曲线的离心率 .
的右焦点,且两条曲线交点的连线过F,则该双曲线的离心率 .
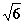 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为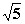 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a + b的最大值为 .
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a + b的最大值为 .