题目内容
19.sin(π-α)=$\frac{1}{7}$,α是第二象限角,则tanα=$\frac{\sqrt{3}}{12}$.分析 利用同角三角函数的基本关系、诱导公式,以及三角函数在各个象限中的符号,求得tanα的值.
解答 解:∵sin(π-α)=$\frac{1}{7}$=sinα,即sinα=$\frac{1}{7}$,
∵α是第二象限角,∴cosα=-$\sqrt{{1-sin}^{2}α}$=-$\frac{4\sqrt{3}}{7}$,则tanα=$\frac{sinα}{cosα}$=-$\frac{1}{4\sqrt{3}}$=-$\frac{\sqrt{3}}{12}$,
故答案为:-$\frac{\sqrt{3}}{12}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
9.点M(x,y)在函数y=-$\sqrt{1-{x}^{2}}$的图象上,则$\frac{y-1}{x}$的取值范围是( )
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
10.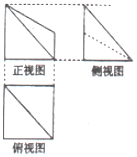 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
 已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )
已知某几何体的三视图如图所示,俯视图中正方形的边长为2,正视图中直角梯形的两底长为1和2,则此几何体的体积为( )| A. | 3 | B. | $\frac{10}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
14.已知Sn为等差数列{an}的前n项和,若a4+a9=10,则S12等于( )
| A. | 30 | B. | 45 | C. | 60 | D. | 120 |
4.执行如图所示的程序框图,若$a=\frac{9}{4}$,则输出S的值为( )
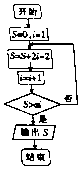

| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
11.点(2,0,3)位于( )
| A. | Y轴上 | B. | X轴上 | C. | XOZ平面内 | D. | YOZ平面内 |
8.A,B,C是球O上的三点,AB=5,AC=3,BC=4,球O的直径等于13,则球心O到平面ABC的距离为( )
| A. | $2\sqrt{3}$ | B. | 6 | C. | 9 | D. | 12 |