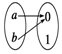
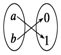
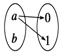
��Ŀ����
2����֪����С��1�ĵȱ�����{an}��ǰn���ΪSn��a1=$\frac{1}{2}��7{a_2}=2{S_3}$����1��������{an}��ͨ�ʽ��
��2����bn=log2��1-Sn+1������$\frac{1}{{{b_1}{b_3}}}+\frac{1}{{{b_3}{b_5}}}+��+\frac{1}{{{b_{2n-1}}{b_{2n+1}}}}=\frac{5}{21}$����n��
���� ��1��������ȣ�������֪����������ȣ�Ȼ��������е�ͨ�ʽ��
��2��������еĺͣ��Ƴ�ͨ�ʽ�������������ʽ���������������⼴�ɣ�
��� �⣺��1����ȱ�����{an}�Ĺ���Ϊq��
��7a2=2S3����5a2=2a1+2a3������2�֣�
��2q2-5q+2=0�����$q=\frac{1}{2}$��q=2����ȥ��������4�֣�
��${a_n}=\frac{1}{2}•{��{\frac{1}{2}}��^{n-1}}={��{\frac{1}{2}}��^n}$����6�֣�
��2����${S_{n+1}}=\frac{{\frac{1}{2}��{1-\frac{1}{{{2^{n+1}}}}}��}}{{1-\frac{1}{2}}}=1-\frac{1}{{{2^{n+1}}}}$������8�֣�
��bn=log2��1-Sn+1��=-n-1������9�֣�
��$\frac{1}{{{b_{2n-1}}{b_{2n+1}}}}=\frac{1}{{��{-2n}����{-2n-2}��}}=\frac{1}{4}��{\frac{1}{n}-\frac{1}{n+1}}��$������10�֣�$\frac{1}{{{b_1}{b_3}}}+\frac{1}{{{b_3}{b_5}}}+��+\frac{1}{{{b_{2n-1}}{b_{2n+1}}}}=\frac{1}{4}[{��{1-\frac{1}{2}}��+��{\frac{1}{2}-\frac{1}{3}}��+��+��{\frac{1}{n}-\frac{1}{n+1}}��}]=\frac{1}{4}��{1-\frac{1}{n+1}}��$������11�֣�
��$\frac{1}{4}��{1-\frac{1}{n+1}}��=\frac{5}{21}$����n=20����12�֣�
���� ��������е�ͨ�ʽ����������ͣ�����ת��˼���Լ�����������

| A�� | 30�� | B�� | 60�� | C�� | 120�� | D�� | 150�� |
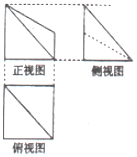 ��֪ij�����������ͼ��ͼ��ʾ������ͼ�������εı߳�Ϊ2������ͼ��ֱ�����ε����׳�Ϊ1��2����˼���������Ϊ��������
��֪ij�����������ͼ��ͼ��ʾ������ͼ�������εı߳�Ϊ2������ͼ��ֱ�����ε����׳�Ϊ1��2����˼���������Ϊ��������| A�� | 3 | B�� | $\frac{10}{3}$ | C�� | $\frac{11}{3}$ | D�� | 4 |
| A�� | ����?x0��R��x${\;}_{0}^{2}$+1��3x0�ķ��ǣ�?x��R��x2+1��3x | |
| B�� | �����ABC�У���A��B����cosA��cosB�ķ������������� | |
| C�� | ƽ������$\overrightarrow{a}$��$\overrightarrow{b}$�ļн��Ƕ۽ǵij�Ҫ�����ǣ�$\overrightarrow{a}$•$\overrightarrow{b}$��0 | |
| D�� | ��=1�Ǻ���f��x��=sin��x-cos��x����С������Ϊ2�еij�ֲ���Ҫ���� |
| A�� | 30 | B�� | 45 | C�� | 60 | D�� | 120 |
| A�� | Y���� | B�� | X���� | C�� | XOZƽ���� | D�� | YOZƽ���� |
| A�� | ���⡰��x��1����x2-3x+2��0������������ǡ���x2-3x+2=0����x=1�� | |
| B�� | ��p�ţ��Vq��Ϊ�����⣬��p��qΪ������ | |
| C�� | ��a��5��b��-5���ǡ�a+b��0���ij�ֲ���Ҫ���� | |
| D�� | ������p��?x��R��x2+x+1��0����Vp��?x0��R��${x_0}^2+{x_0}+1=0$ |