题目内容
8.已知a,b均为正数,且a2+$\frac{1}{4}$b2=1,则a$\sqrt{1+{b}^{2}}$的最大值为$\frac{5}{4}$.分析 得到4a2+b2=4,根据不等式的性质通过放大不等式求出最大值即可.
解答 解:∵a,b均为正数,且a2+$\frac{1}{4}$b2=1,
∴4a2+b2=4,
∴a$\sqrt{1+{b}^{2}}$=$\frac{1}{2}$•2a•$\sqrt{1{+b}^{2}}$≤$\frac{1}{2}$•$\frac{{4a}^{2}+1{+b}^{2}}{2}$=$\frac{5}{4}$,
当且仅当4a2=b2+1即a=$\frac{\sqrt{10}}{4}$,b=$\frac{\sqrt{6}}{2}$时“=”成立,
故答案为:$\frac{5}{4}$.
点评 本题考查了基本不等式的性质,考查转化思想,是一道基础题.

练习册系列答案
相关题目
6.若(1-2x)6=a0+a1x+a2x+…+a6x6,则|a0|+|a1|+|a2|+…+|a6|的值为( )
| A. | 1 | B. | 26 | C. | 35 | D. | 36 |
20.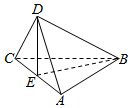 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
18.若m为实数且(2+mi)(m-2i)=-4-3i,则m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |