题目内容
13.设实数a<0,定义域为R的函数$f(x)=a{cos^2}x-bsinxcosx-\frac{a}{2}$的最大值是$\frac{1}{2}$,且$f(\frac{π}{3})=\frac{{\sqrt{3}}}{4}$,(1)求a、b的值;
(2)求函数f(x)在$x∈[\frac{π}{4},\frac{3π}{4}]$上的最值.
分析 (1)利用倍角公式降幂,再由已知得关于a,b的不等式组,求解不等式组得a,b的值;
(2)由(1)得函数解析式,再由x的范围求得相位的范围,则函数f(x)在$x∈[\frac{π}{4},\frac{3π}{4}]$上的最值可求.
解答 解:(1)$f(x)=a{cos^2}x-bsinxcosx-\frac{a}{2}$=$\frac{a(1+cos2x)}{2}-\frac{b}{2}sin2x$$-\frac{a}{2}$
=$\frac{a}{2}cos2x-\frac{b}{2}sin2x$,
由题意得:$\left\{\begin{array}{l}{\frac{a}{4}^2}+{\frac{b}{4}^2}=\frac{1}{4}\\-\frac{a}{4}-\frac{{\sqrt{3}b}}{4}=\frac{{\sqrt{3}}}{4}\end{array}\right.$,解得:$\left\{\begin{array}{l}a=-\frac{{\sqrt{3}}}{2}\\ b=-\frac{1}{2}\end{array}\right.$;
(2)由(1)得:$f(x)=-\frac{{\sqrt{3}}}{4}cos2x+\frac{1}{4}sin2x=\frac{1}{2}sin(2x-\frac{π}{3})$,
∵$x∈[\frac{π}{4},\frac{3π}{4}]$,
∴$2x-\frac{π}{3}∈[\frac{π}{6},\frac{7π}{6}]$,
故当$2x-\frac{π}{3}=\frac{π}{2}$,即$x=\frac{5π}{12}$时,函数f(x)的最大值为$\frac{1}{2}$;
当$2x-\frac{π}{3}=\frac{7π}{6}$,即$x=\frac{3π}{4}$时,函数f(x)的最小值为$-\frac{1}{4}$.
点评 本题考查三角函数中的恒等变换应用,考查了y=Asin(ωx+φ)型函数的图象和性质,是中档题.

| A. | 直线y=-$\frac{1}{2}$x | B. | 直线y=$\frac{1}{2}$x | C. | 直线y=-$\frac{1}{2}$ | D. | 直线x=-$\frac{1}{2}$ |
 如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.
如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.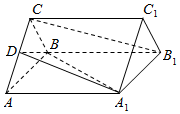 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.