题目内容
19.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的两个焦点是F1,F2,点P在该椭圆上,若PF1-PF2=2,则△PF1F2的面积是$\sqrt{2}$.分析 利用椭圆的定义,求得|PF1|=3,|PF2|=1,则△PF2F1是直角三角形,即可求得△PF1F2的面积.
解答 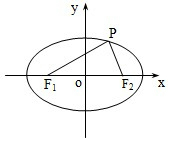 解:∵$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,焦点在x轴上,则a=2,由椭圆定义:|PF1|+|PF2|=4,丨F1F2丨=2c=2$\sqrt{2}$,
解:∵$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,焦点在x轴上,则a=2,由椭圆定义:|PF1|+|PF2|=4,丨F1F2丨=2c=2$\sqrt{2}$,
∵|PF1|-|PF2|=2,可得|PF1|=3,|PF2|=1,
由12+(2$\sqrt{2}$)2=9,
∴△PF2F1是直角三角形,
△PF1F2的面积$\frac{1}{2}$|PF2|×|F1F2|=$\frac{1}{2}$×1×2$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查椭圆的标准方程,椭圆的定义,考查计算能力,属于中档题.

练习册系列答案
相关题目
12.某市为鼓励居民节约用水,将实行阶梯水价,该市每户居民每月用水量划分为三级,水价实行分级递增.第一级水量:用水量不超过20吨,水价标准为1.5元/吨; 第二级水量:用水量超过20但不超过30吨,超出第一级水量的部分,水价为2.25元/吨; 第三级水量:用水量超过30吨,超出第二级水量的部分,水价为3.0元/吨.随机调查了该市1000户居民,获得了他们某月的用水量数据,整理得到如下的频率分布表:
(Ⅰ)根据频率分布表中的数据,写出a,b,c的值;从该市调查的1000户居民中随机抽取一户居民,求该户居民用水量不超过30吨的概率;
(Ⅱ)从1000户居民中按用水三个等级分层抽取5户幸运者,发给大奖两份和幸运奖三份共5份,每户一份,求两份大奖获得者的都是节水型用户(用水量不超过20吨的居民)的概率.
| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
(Ⅱ)从1000户居民中按用水三个等级分层抽取5户幸运者,发给大奖两份和幸运奖三份共5份,每户一份,求两份大奖获得者的都是节水型用户(用水量不超过20吨的居民)的概率.
8.已知a,b为正实数,且$\frac{1}{a}$+$\frac{2}{b}$=2,若a+b≥c对满足条件的a,b恒成立,则c的取值范围是( )
| A. | (-∞,$\frac{3}{2}$+$\sqrt{2}$] | B. | (-∞,3] | C. | (-∞,6] | D. | (-∞,3+2$\sqrt{2}$] |
8.四面体PABC的四个顶点都在球O的球面上,PA=8,BC=4,PB=PC=AB=AC,且平面PBC⊥平面ABC,则球O的表面积为( )
| A. | 64π | B. | 65π | C. | 66π | D. | 128π |