题目内容
14.四面体A-BCD中,AB=AC=DB=DC=2$\sqrt{6}$,AD=BC=4,则它的外接球表面积等于32π.分析 如图,取BC、AD中点分别为E、F,连结DE,AE,EF,取EF中点O,AO=DO=OB=OC=2$\sqrt{2}$,即可得O为四面体A-BCD的外接球,半径R=2$\sqrt{2}$,
解答  解:如图,取BC、AD中点分别为E、F,连结DE,AE,EF,
解:如图,取BC、AD中点分别为E、F,连结DE,AE,EF,
∵AB=AC=DB=DC=2$\sqrt{6}$,∴AE⊥BC,DE⊥BC,∴AE=DE$\sqrt{A{B}^{2}-B{E}^{2}}=2\sqrt{5}$,∴EF⊥AD,
取EF中点O,OF=$\frac{1}{2}\sqrt{A{E}^{2}-A{F}^{2}}=2$,∴AO=DO=$\sqrt{O{F}^{2}+A{F}^{2}}=2\sqrt{2}$,
同理可得OB=OC=2$\sqrt{2}$,故O为四面体A-BCD的外接球,半径R=2$\sqrt{2}$,
则它的外接球表面积等于4πR2=32π,
故答案为:32π.
点评 本题考查了四面体外接球的表面积,解题关键是找到球心,求出半径,属于中档题.

练习册系列答案
相关题目
6.已知x、y满足约束条件$\left\{\begin{array}{l}{x-2y+7≥0}\\{4x-3y-12≤0}\\{x+2y-3≥0}\end{array}\right.$,则Z=x2+y2+2x+1的最小值是( )
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{16}{5}$ | C. | 2$\sqrt{41}$ | D. | 164 |
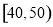 ,
,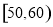 ,…,
,…,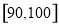 后得到如下频率分布直方图.
后得到如下频率分布直方图.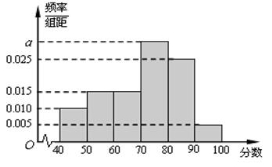
 内的频率;
内的频率;