题目内容
12.某市为鼓励居民节约用水,将实行阶梯水价,该市每户居民每月用水量划分为三级,水价实行分级递增.第一级水量:用水量不超过20吨,水价标准为1.5元/吨; 第二级水量:用水量超过20但不超过30吨,超出第一级水量的部分,水价为2.25元/吨; 第三级水量:用水量超过30吨,超出第二级水量的部分,水价为3.0元/吨.随机调查了该市1000户居民,获得了他们某月的用水量数据,整理得到如下的频率分布表:| 用水量(吨) | [0,10] | (10,20] | (20,30] | (30,40] | (40,50] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
(Ⅱ)从1000户居民中按用水三个等级分层抽取5户幸运者,发给大奖两份和幸运奖三份共5份,每户一份,求两份大奖获得者的都是节水型用户(用水量不超过20吨的居民)的概率.
分析 (Ⅰ)由频率=$\frac{频数}{总数}$,能求出a,b,c.设“该户居民月用水量不超过30吨”为事件A,利用互斥事件概率加法公式能求出该居民月用水量不超过30吨的概率.
(Ⅱ)设“获得两份大奖的都是节水型用户”为事件B.由分层抽样可得,第一级抽取了3人,记为a1,a2,a3,第二级抽取1人,记为b,第三级抽取1人,记为c,利用列举法能求出两份大奖获得者的都是节水型用户的概率.
解答 解:(Ⅰ)由意知$\left\{\begin{array}{l}{\frac{400}{1000}=a}\\{\frac{b}{1000}=0.1}\\{\frac{100}{1000}=c}\end{array}\right.$,解得a=0.4,b=100,c=0.1.…(3分)
设“该户居民月用水量不超过30吨”为事件A.
由表可知:所以该居民月用水量不超过30吨的概率:
P(A)=0.2+0.4+0.2=0.8.…(4分)
(Ⅱ)设“获得两份大奖的都是节水型用户”为事件B.
由分层抽样可得,第一级抽取了3人,记为a1,a2,a3,第二级抽取1人,记为b,
第三级抽取1人,记为c(6分)
则所有基本事件为:(a1,a2),(a1,a3),(a2,a3),(a1,b),
(a1,c),(a2,b),(a2,c),(a3,b),(a3,c),(b,c)共10种 (8分)
事件B所包含的基本事件有:(a1,a2),(a1,a3),(a2,a3)共3种
则P(B)=$\frac{3}{10}$,
所以两份大奖获得者的都是节水型用户的概率为$\frac{3}{10}$.(12分)
点评 本题考查频率分布表的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
17.计算lg4+lg25=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 10 |
20. 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
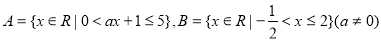 .
.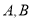 能否相等?若能,求出实数
能否相等?若能,求出实数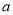 的值;若不能,试说明理由;
的值;若不能,试说明理由;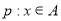 ,命题
,命题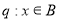 ,且
,且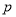 是
是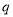 充分不必要条件,求实数
充分不必要条件,求实数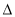 ABC的三边为a,b,c.其面积S=
ABC的三边为a,b,c.其面积S= 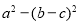 ,且b+c=8.
,且b+c=8.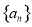 的前
的前 项和为
项和为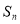 ,且
,且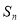
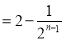 ,
,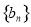 为等差数列,且
为等差数列,且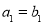 ,
,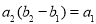 .
.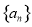 和
和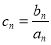 ,求数列
,求数列 的前
的前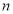 项和
项和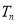 .
.