题目内容
17.设函数f(x0)=aexlnx+$\frac{b{e}^{x-1}}{x}$,曲线y=f(x)在点(1,f(1)处的切线为y=e(x-1)+2.(Ⅰ)求a,b;
(Ⅱ)证明:f(x)>1.
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1),求出a,b的值即可;
(Ⅱ)问题等价于$xlnx>x{e^{-x}}-\frac{2}{e}$,设函数g(x)=xlnx,设函数$h(x)=x{e^{-x}}-\frac{2}{e}$,根据函数的单调性证明即可.
解答 解:(Ⅰ) 函数f(x)的定义域为(0,+∞),
$f'(x)=a{e^x}lnx+\frac{a}{x}{e^x}-\frac{b}{x^2}{e^{x-1}}+\frac{b}{x}{e^{x-1}}$,
由题意可得f(1)=2,f'(1)=e,
故a=1,b=2…(6分)
(Ⅱ)证明:由(Ⅰ)知,?$f(x)={e^x}lnx+\frac{{2{e^{x-1}}}}{x}$,
从而f(x)>1等价于$xlnx>x{e^{-x}}-\frac{2}{e}$,
设函数g(x)=xlnx,则g'(x)=1+lnx,
所以当$x∈({0,\frac{1}{e}})$时,g'(x)<0,
当$x∈({\frac{1}{e},+∞})$时,g'(x)>0,
故g(x)在$({0,\frac{1}{e}})$单调递减,在$({\frac{1}{e},+∞})$单调递增,
从而g(x)在(0,+∞)的最小值为$g(\frac{1}{e})=-\frac{1}{e}$.…(8分)
设函数$h(x)=x{e^{-x}}-\frac{2}{e}$,则h'(x)=e-x(1-x),
所以当x∈(0,1)时,h'(x)>0,
当x∈(1,+∞)时,h'(x)<0,
故h(x)在(0,1)单调递增,在(1,+∞)单调递减,
从而h(x)在(0,+∞)的最大值为$h(1)=-\frac{1}{e}$.
综上:当x>0时,g(x)>h(x),即f(x)>1.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道中档题.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | p假q假 | B. | p假q真 | C. | p真q假 | D. | p真q真 |
| A. | $\frac{f(2)}{f(0)}>2,\frac{f(0)}{{f({-2})}}>2$ | B. | f(2)>2f(0)>4f(-2) | C. | $\frac{f(2)}{f(0)}<2,\frac{f(0)}{{f({-2})}}<2$ | D. | f(2)<2f(0)<4f(-2) |
| x | 2 | 3 | 4 | 7 | 9 |
| y | 26 | 33 | m | 54 | 75 |
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
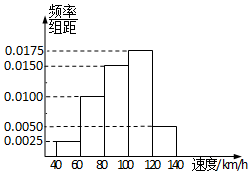 根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.
根据某固定测速点测得的某时段内过往的200辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h-120km/h,则该时段内非正常行驶的机动车辆数为30.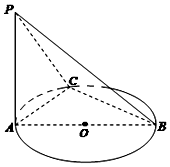 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则二面角A-BC-P的大小为( )