题目内容
设圆x2+y2=4的一条切线与x轴、y轴分别交于点A、B,则|AB|的最小值为( )
| A、4 | ||
B、4
| ||
| C、6 | ||
| D、8 |
考点:圆的标准方程
专题:直线与圆
分析:设切线方程为
+
=1,由圆心到直线的距离等于半径得2
≤
,令 t=
,则t2-4t≥0,由此求得t的最小值为4,即为所求.
| x |
| a |
| y |
| b |
| a2+b2 |
| a2+b2 |
| 2 |
| a2+b2 |
解答:
解:设切线方程为
+
=1,即 bx+ay-ab=0,由圆心到直线的距离等于半径得
=2,∴|a||b|=2
≤
,令 t=
,
则t2-4t≥0,t≥4,故t的最小值为4.由题意知t=|AB|,
故答案为:4.
| x |
| a |
| y |
| b |
| |0+0-ab| | ||
|
| a2+b2 |
| a2+b2 |
| 2 |
| a2+b2 |
则t2-4t≥0,t≥4,故t的最小值为4.由题意知t=|AB|,
故答案为:4.
点评:本题考查点到直线的距离公式和基本不等式的应用,体现了换元的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“a=3”是“函数f(x)=|3x-a|在[1,+∞)上为单调递增函数的”( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知i是虚数单位,m∈R,且
是纯虚数,则(
)2008等于( )
| 2-mi |
| 1+i |
| 2-mi |
| 2+mi |
| A、1 | B、-1 | C、i | D、-i |
不等式
<1的解集是( )
| 2 |
| x+1 |
| A、(-∞,-1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、(-1,1) |
“a>m>1”是“logam<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
过抛物线y2=4x的焦点作直线l交抛物线于A、B两点,若线段AB中点的横坐标为5,则|AB|等于( )
| A、12 | B、8 | C、6 | D、4 |
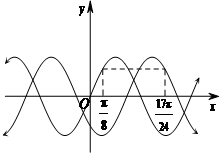 已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )
已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<x)个单位得到,这两个函数的部分图象如图所示,则φ=( )A、
| ||
B、
| ||
C、
| ||
D、
|