题目内容
10.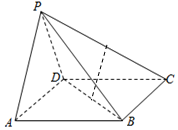 如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.(1)证明:EF∥平面PAD;
(2)证明:直线PA⊥平面PCD.
分析 (1)根据线面平行的判定定理进行证明即可.
(2)证明CD⊥PA,PA⊥PD,运用线面垂直的定理可证明.
解答  证明:(1)连结AC,则F也是AC的中点,
证明:(1)连结AC,则F也是AC的中点,
又E是PC的中点,∴EF∥PA,
又EF?平面PAD,PA?平面PAD,
∴EF∥平面PAD;
(2)∵平面PAD⊥平面ABCD,CD⊥AD,面PAD∩面ABCD=AD,∴CD⊥面PAD,
∵PA?面PAD,∴CD⊥PA,
∵∠APD=90°,
∴PA⊥PD,
∵CD∩PD=D,
∴PA⊥平面PCD
点评 本题主要考查空间直线和平面平行、垂直的判定,根据相应的判定定理是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若f(x)=f′(1)x2+ex,则f(1)=( )
| A. | e | B. | 0 | C. | e+1 | D. | e-1 |
18.设f(x)是R上的奇函数f(x+4)=f(x),当x∈[0,1]时,f(x)=3x,则f(11.5)=( )
| A. | 1.5 | B. | 0.5 | C. | -1.5 | D. | -0.5 |
2.已知命题p:?x0∈R,x02+2x0+2≤0,则命题p的否定?p是( )
| A. | ?p:?x0∈R,x02+2x0+2>0 | B. | ¬p:?x∈R,x2+2x+2>0 | ||
| C. | ?p:?x0∈R,x02+2x0+2≥0 | D. | ?p:?x∈R,x2+2x+2≥0 |
19.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等比数列,则公比q等于( )
| A. | 2 | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
20.已知点(x,y)满足不等式组$\left\{\begin{array}{l}x-y+3≥0\\ 2x-y-1≤0\\ 3x+2y-6≥0\end{array}\right.$,则z=x+y的最小值为( )
| A. | 3 | B. | 11 | C. | $\frac{17}{7}$ | D. | $\frac{15}{7}$ |