题目内容
15.函数y=logax,y=ax,y=x+a在同一坐标系中的图象可能是( )| A. | 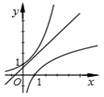 | B. |  | C. | 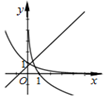 | D. | 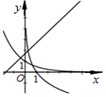 |
分析 根据指数函数,对数函数和一次函数的图象和性质分别进行判断即可.
解答 解:对于A:由指数函数和对数函数的单调性可知a>1,此时直线y=x+a的截距不满足条件.
对于B:指数函数和对数函数的单调性不相同,不满足条件.
对于C:由指数函数和对数函数的单调性可知0<a<1,此时直线y=x+a的截距满足条件.
对于D:由指数函数和对数函数的单调性可知0<a<1,此时直线y=x+a的截距a>1不满足条件.
故选:C.
点评 本题主要考查函数图象的识别和判断,要求熟练掌握指数函数和对数函数的图象和性质,比较基础.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
5.定义域为R的函数f(x)满足f(x+1)=2f(x),且当x∈[0,1]时,f(x)=x2-x,则当x∈[-2,-1]时,f(x)的最小值为( )
| A. | -$\frac{1}{16}$ | B. | -$\frac{1}{8}$ | C. | -$\frac{1}{4}$ | D. | 0 |
6.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>3)=0.023,则P(-3≤ξ≤3)=( )
| A. | 0.954 | B. | 0.023 | C. | 0.977 | D. | 0.046 |
7.已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an,使得$\sqrt{{a_m}{a_n}}=4{a_1}$,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
4.函数y=(3-x2)ex的单调递增区间是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-3) | D. | (-3,1) |
5.若函数f(x)=x2ex-a恰有三个零点,则实数a的取值范围是( )
| A. | $({\frac{4}{e^2},+∞})$ | B. | $({0,\frac{4}{e^2}})$ | C. | (0,4e2) | D. | (0,+∞) |
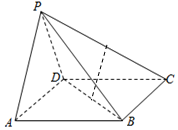 如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.