题目内容
2.已知命题p:?x0∈R,x02+2x0+2≤0,则命题p的否定?p是( )| A. | ?p:?x0∈R,x02+2x0+2>0 | B. | ¬p:?x∈R,x2+2x+2>0 | ||
| C. | ?p:?x0∈R,x02+2x0+2≥0 | D. | ?p:?x∈R,x2+2x+2≥0 |
分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以命题p:“?x0∈R,x02+2x0+2≤0”,
则命题p的否定¬p是:?x∈R,x2+2x+2>0.
故选:B
点评 本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.由经验得知,在某大商场付款处排队等候付款的人数及其概率如表:
(1)不多于6个人排队的概率;
(2)至少8个人排队的概率.
| 排队人数 | 5人及以下 | 6 | 7 | 8 | 9 | 10人及以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(2)至少8个人排队的概率.
7.已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an,使得$\sqrt{{a_m}{a_n}}=4{a_1}$,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
11.数列1,3,6,10,…的通项公式是( )
| A. | ${a_n}={n^2}-({n-1})$ | B. | ${a_n}={n^2}-1$ | C. | ${a_n}=\frac{{n({n+1})}}{2}$ | D. | ${a_n}={n^2}+1$ |
12.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
y关于t的线性回归方程为$\widehaty=0.5t+2.3$,则a的值为4.8.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | a | 5.2 | 5.9 |
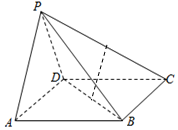 如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.