题目内容
19.已知等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等比数列,则公比q等于( )| A. | 2 | B. | $1-\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3-2\sqrt{2}$ |
分析 利用等比数列通项公式及等比数列性质列出方程,由此能求出公比.
解答 解:∵等比数列{an}中,各项都是正数,且${a_1},\frac{1}{2}{a_3},2{a_2}$成等比数列,
∴$\left\{\begin{array}{l}{(\frac{1}{2}{a}_{1}{q}^{2})^{2}={a}_{1}(2{a}_{1}q)}\\{q>0}\end{array}\right.$,
解得q=2.
故选:A.
点评 本题考查等差数列的公比的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
9.已知向量$\overrightarrow a=({1-t,2t-1,3})$,$\overrightarrow b=({2,t,t})$,则$|{\overrightarrow a-\overrightarrow b}|$的最小值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
7.已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an,使得$\sqrt{{a_m}{a_n}}=4{a_1}$,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
4.函数y=(3-x2)ex的单调递增区间是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-3) | D. | (-3,1) |
11.数列1,3,6,10,…的通项公式是( )
| A. | ${a_n}={n^2}-({n-1})$ | B. | ${a_n}={n^2}-1$ | C. | ${a_n}=\frac{{n({n+1})}}{2}$ | D. | ${a_n}={n^2}+1$ |
8.已知函数f(x)=m(x+m+3)(x+m+2),g(x)=2x-2,若?x∈R,f(x)<0或g(x)<0恒成立,则实数m的取值范围为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-3,-2) | D. | (0,3) |
9.已知△ABC中,a=1,$b=\sqrt{3}$,A=30°,则B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
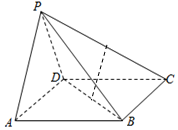 如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.