题目内容
18.设f(x)是R上的奇函数f(x+4)=f(x),当x∈[0,1]时,f(x)=3x,则f(11.5)=( )| A. | 1.5 | B. | 0.5 | C. | -1.5 | D. | -0.5 |
分析 先根据题意分析可得函数f(x)的周期为4,可得f(11.5)=f(-0.5+4×3)=f(-0.5),在结合函数的奇偶性可得f(-0.5)=-f(0.5),结合函数的解析式可得f(0.5)的值,综合可得答案.
解答 解:根据题意,函数f(x)满足f(x+4)=f(x),即函数的周期为4,
则有f(11.5)=f(-0.5+4×3)=f(-0.5),
又由函数为奇函数,则f(-0.5)=-f(0.5),
又由x∈[0,1]时,f(x)=3x,则f(0.5)=3×0.5=1.5;
故f(11.5)=f(-0.5)=-f(-0.5)=-1.5;
故选:C.
点评 本题考查函数的奇偶性、周期性,关键是利用函数的周期性、奇偶性分析得到f(11.5)与f(0.5)的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知向量$\overrightarrow a=({1-t,2t-1,3})$,$\overrightarrow b=({2,t,t})$,则$|{\overrightarrow a-\overrightarrow b}|$的最小值为( )
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $2\sqrt{2}$ |
6.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>3)=0.023,则P(-3≤ξ≤3)=( )
| A. | 0.954 | B. | 0.023 | C. | 0.977 | D. | 0.046 |
13.由经验得知,在某大商场付款处排队等候付款的人数及其概率如表:
(1)不多于6个人排队的概率;
(2)至少8个人排队的概率.
| 排队人数 | 5人及以下 | 6 | 7 | 8 | 9 | 10人及以上 |
| 概率 | 0.1 | 0.16 | 0.3 | 0.3 | 0.1 | 0.04 |
(2)至少8个人排队的概率.
7.已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an,使得$\sqrt{{a_m}{a_n}}=4{a_1}$,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
8.已知函数f(x)=m(x+m+3)(x+m+2),g(x)=2x-2,若?x∈R,f(x)<0或g(x)<0恒成立,则实数m的取值范围为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-3,-2) | D. | (0,3) |
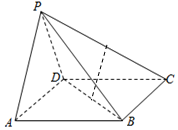 如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为矩形,△PAD为等腰三角形,∠APD=90°,平面PAD⊥平面ABCD,且AB=1,AD=2,E,F分别为PC,BD的中点.