题目内容
11．若f（x）=f′（1）x2+ex，则f（1）=（ ）| A． | e | B． | 0 | C． | e+1 | D． | e-1 |
分析 由f（x）=f′（1）x2+ex，求导得：f′（x）=2f′（1）x+ex，令x=1，解得f′（1）=-e．f（x）=-ex2+ex，可得
f（1）．
解答 解：由f（x）=f′（1）x2+ex，
求导得：f′（x）=2f′（1）x+ex，令x=1可得，f′（1）=2f′（1）+e，解得f′（1）=-e．
∴f（x）=-ex2+ex，∴f（1）=-e+e=0．
故选：B．
点评 本题考查了导数的运算法则、方程的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
5．定义域为R的函数f（x）满足f（x+1）=2f（x），且当x∈[0，1]时，f（x）=x2-x，则当x∈[-2，-1]时，f（x）的最小值为（ ）
| A． | -$\frac{1}{16}$ | B． | -$\frac{1}{8}$ | C． | -$\frac{1}{4}$ | D． | 0 |
9．已知向量$\overrightarrow a=（{1-t，2t-1，3}）$，$\overrightarrow b=（{2，t，t}）$，则$|{\overrightarrow a-\overrightarrow b}|$的最小值为（ ）
| A． | 2 | B． | $\sqrt{5}$ | C． | $\sqrt{6}$ | D． | $2\sqrt{2}$ |
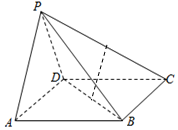如图所示，在四棱锥P-ABCD中，四边形ABCD为矩形，△PAD为等腰三角形，∠APD=90°，平面PAD⊥平面ABCD，且AB=1，AD=2，E，F分别为PC，BD的中点．