��Ŀ����
18��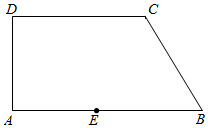 ��ͼ��һ��ֱ��������ABCD��AB��CD����BAD=90�㣬�����AB=14m��CD=10m����ABC=60�㣬����߶�AB��һ��E���һ��ֱ·EF����F���ı���ABCD�ı��ϣ�����·�Ŀ��ȣ��������ط�Ϊ���֮��Ϊ3��1����ʯ�����ֱַ���ֲ��ͬ���ܣ���EB=x��EF=y����λ��m��
��ͼ��һ��ֱ��������ABCD��AB��CD����BAD=90�㣬�����AB=14m��CD=10m����ABC=60�㣬����߶�AB��һ��E���һ��ֱ·EF����F���ı���ABCD�ı��ϣ�����·�Ŀ��ȣ��������ط�Ϊ���֮��Ϊ3��1����ʯ�����ֱַ���ֲ��ͬ���ܣ���EB=x��EF=y����λ��m����1������F���C�غ�ʱ����ȷ����E��λ�ã�
��2����y����x�ĺ�����ϵʽ��
��3����ȷ����E��F��λ�ã�ʹֱ·EF������̣�
���� ��1����F���C�غ�ʱ��������������ε�������������֮�Ƚ������̹�ϵ���ɵõ����ۣ�
��2����EB=x��EF=y���������֮�Ƚ������̹�ϵ�������������ɣ�
��3������һԪ���κ�������ֵ���ʣ����EF����ֵ�����ɵõ����ۣ�
��� �⣺��1������F���C�غ�ʱ��h=CO=$\sqrt{3}$��14-10��=4$\sqrt{3}$��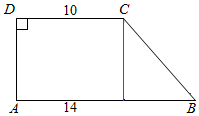
�ı���DABC�����S1=$\frac{��14-x��+10}{2}��4\sqrt{3}$=2$\sqrt{3}$��24-x����
��CEB�����S2=$\frac{4\sqrt{3}x}{2}$=2$\sqrt{3}$x��
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{2\sqrt{3}��24-x��}{2\sqrt{3}x}$=$\frac{3}{1}$����24-x=3x��
��4x=24��x=6��
��BE=6��AE=8��
��2���ı���DAEF�����S1=$\frac{[��14-x��+��14-x��+\sqrt{{y}^{2}-48}]��4\sqrt{3}}{2}$=$\frac{��28-2x+\sqrt{{y}^{2}-48}��}{2}��4\sqrt{3}$=2$\sqrt{3}$��28-2x+$\sqrt{{y}^{2}-48}$����
�ı���FEBC�����S2=$\frac{[��x-4��-\sqrt{{y}^{2}+48}+x]��4\sqrt{3}}{2}$=2$\sqrt{3}$��2x-4-$\sqrt{{y}^{2}-48}$����
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{3}{1}$����S1=3S2��
��2$\sqrt{3}$��28-2x+$\sqrt{{y}^{2}-48}$��=3��2$\sqrt{3}$��2x-4-$\sqrt{{y}^{2}-48}$
��28-2x+$\sqrt{{y}^{2}-48}$=6x-12-3$\sqrt{{y}^{2}-48}$����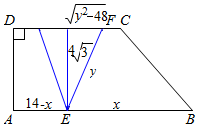
��4$\sqrt{{y}^{2}-48}$=8x-40��
��y2=4x2-40x+148����y=$\sqrt{4{x}^{2}-40x+148}$=2$\sqrt{{x}^{2}-10x+37}$��
��3����y=2$\sqrt{{x}^{2}-10x+37}$=2$\sqrt{��x-5��^{2}+12}$��
�൱x=5ʱ��y��СΪy=2$\sqrt{12}$=4$\sqrt{3}$����ʱEF����СֵΪ4$\sqrt{3}$��
��ʱBE=5��AE=9��FC=1��DF=9��
���� ������Ҫ���麯����Ӧ�����⣬���������������̹�ϵ�ǽ������Ĺؼ����ۺ��Խ�ǿ����һ�����Ѷȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | ��$\sqrt{2}$��$\sqrt{6}$�� | B�� | ��$\sqrt{2}$��$\sqrt{7}$�� | C�� | ��2��$\sqrt{6}$�� | D�� | ��2��$\sqrt{7}$�� |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
| A�� | $\frac{7}{18}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{6}$ | D�� | $\frac{5}{18}$ |
| A�� | 1 | B�� | 8 | C�� | -1��9 | D�� | 1��-9 |
| A�� | [-$\frac{1}{3}$��$\frac{3}{2}$] | B�� | ��-$\frac{1}{3}$��$\frac{3}{2}$] | C�� | ��-2��$\frac{3}{2}$] | D�� | [$\frac{3}{2}$��2�� |
 ��ͼ��ʾ����Ҷͼ��¼�˼ס������������ͬѧ���ij����ѧ��ĵ÷��������������Ϊ12�֣���֪�ס��������ƽ���ɼ���ͬ������ij�����ݵĸ�λ��ģ������Ϊx��
��ͼ��ʾ����Ҷͼ��¼�˼ס������������ͬѧ���ij����ѧ��ĵ÷��������������Ϊ12�֣���֪�ס��������ƽ���ɼ���ͬ������ij�����ݵĸ�λ��ģ������Ϊx��