题目内容
3. 如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况,该题满分为12分.已知甲、乙两组的平均成绩相同,乙组某个数据的个位数模糊,记为x.
如图所示,茎叶图记录了甲、乙两组各四名同学完成某道数学题的得分情况,该题满分为12分.已知甲、乙两组的平均成绩相同,乙组某个数据的个位数模糊,记为x.(Ⅰ)求x的值,并判断哪组学生成绩更稳定;
(Ⅱ)在甲、乙两组中各抽出一名同学,求这两名同学的得分之和低于20分的概率.
分析 (Ⅰ)根据两组数据的平均数相等,可得x的值,进而求出两组数据的方差,比较可得哪组学生成绩更稳定;
(Ⅱ)分别计算在甲、乙两组中各抽出一名同学及成绩和低于20分的取法种数,代入古典概型概率公式,可得答案
解答 解:(Ⅰ)$\overline{{x}_{甲}}$=$\frac{1}{4}$(9+9+11+11)=10,
$\overline{{x}_{乙}}$=$\frac{1}{4}$(8+9+10+x+12)=10,
解得:x=1
又S甲2=$\frac{1}{4}$[(9-10)2+(9-10)2+(11-10)2+(11-10)2]=1;
S乙2=$\frac{1}{4}$[(8-10)2+(9-10)2+(11-10)2+(12-10)2]=$\frac{5}{2}$,
∴S甲2<S乙2,
∴甲组成绩比乙组稳定.
(Ⅱ)记甲组4名同学为:A1,A2,A3,A4;乙组4名同学为:B1,B2,B3,B4;
分别从甲乙两组中各抽取一名同学所有可能的结果为:
(A1,B1),(A1,B2),(A1,B3),(A1,B4)
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),共16个基本事件,
其中得分之和低于(20分)的共6个基本事件,
∴得分之和低于(20分)的概率是:P=$\frac{6}{16}$=$\frac{3}{8}$.
点评 本题考查了古典概型概率计算公式,茎叶图,掌握古典概型概率公式:概率=所求情况数与总情况数之比是解题的关键.

练习册系列答案
相关题目
14.已知α∈(-π,-$\frac{π}{4}$),且sinα=-$\frac{1}{3}$,则cosα等于( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | ±$\frac{2\sqrt{2}}{3}$ | D. | $\frac{2}{3}$ |
11.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,收集数据如表所示:
根据表可得回归方程$\hat y=\hat bx+\hat a$中的$\hat b$为9.4,据此可估计加工零件数为6时加工时间大约为( )
| 零件数x(个) | 2 | 3 | 4 | 5 |
| 加工时间y(min) | 26 | 39 | 49 | 54 |
| A. | 63.6min | B. | 65.5min | C. | 67.7min | D. | 72.0min |
12.下列函数在其定义域内既是奇函数又是增函数的是( )
| A. | y=2-x | B. | y=x3+x | C. | y=-$\frac{1}{x}$ | D. | y=lnx |
10.4sin80°-$\frac{cos10°}{sin10°}$等于( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$-3 |
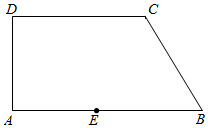 如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)
如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)