题目内容
6．复数z=$\frac{1-3i}{i-1}$在复平面上所对应的点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 利用复数代数形式的乘除运算化简，求出z所对应点的坐标得答案．
解答 解：$z=\frac{1-3i}{i-1}$=$\frac{（1-3i）（-1-i）}{（-1+i）（-1-i）}=\frac{-4+2i}{2}=-2+i$，
∴复数$z=\frac{1-3i}{i-1}$在复平面上所对应的点的坐标为（-2，1），位于第二象限，
故选：B．
点评 本题考查复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
19．某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[50，100]内，发布成绩使用等级制．各等级划分标准见表．规定：A．B．C三级为合格等级，D为不合格等级．
为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计．按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图1所示，样本中原始成绩在80分及以上的所有数据的茎叶图如图2所示．
（I）求n和频率分布直方图中的x，y的值；并估计该校高一年级学生成绩是合格等级的概率；
（Ⅱ）在选取的样本中，从A、D两个等级的学生中随机抽取了2名学生进行调研，求至少有一名学生是A等级的概率．
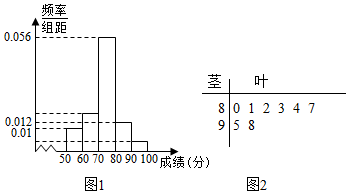
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
（I）求n和频率分布直方图中的x，y的值；并估计该校高一年级学生成绩是合格等级的概率；
（Ⅱ）在选取的样本中，从A、D两个等级的学生中随机抽取了2名学生进行调研，求至少有一名学生是A等级的概率．
14．已知α∈（-π，-$\frac{π}{4}$），且sinα=-$\frac{1}{3}$，则cosα等于（ ）
| A． | -$\frac{2\sqrt{2}}{3}$ | B． | $\frac{2\sqrt{2}}{3}$ | C． | ±$\frac{2\sqrt{2}}{3}$ | D． | $\frac{2}{3}$ |
11．一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了4次试验，收集数据如表所示：
根据表可得回归方程$\hat y=\hat bx+\hat a$中的$\hat b$为9.4，据此可估计加工零件数为6时加工时间大约为（ ）
| 零件数x（个） | 2 | 3 | 4 | 5 |
| 加工时间y（min） | 26 | 39 | 49 | 54 |
| A． | 63.6min | B． | 65.5min | C． | 67.7min | D． | 72.0min |
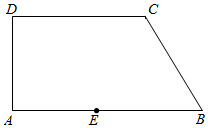如图是一块直角梯形园地ABCD，AB∥CD，∠BAD=90°，经测最，AB=14m，CD=10m，∠ABC=60°，拟过线段AB上一点E设计一条直路EF（点F在四边形ABCD的边上，不计路的宽度），将该园地分为面积之比为3：1的左、石两部分分别种植不同花卉．设EB=x，EF=y（单位：m）