题目内容
13.若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,则点P在直线x+y=6下方的概率是( )| A. | $\frac{7}{18}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{18}$ |
分析 连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,共可得到6×6=36个点,由横纵坐标的和小于6得到点P在直线x+y=6下方的点的个数,然后由古典概型概率计算公式得答.
解答 解:连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,共可得到6×6=36个点,
点P在直线x+y=6下方的情况有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(3,1),(3,2),(4,1),10种,
故点P在直线x+y=6下方的概率为$\frac{10}{36}$=$\frac{5}{18}$,
故选:D.
点评 本题考查了等可能事件的概率,考查了古典概型及其概率计算公式,是基础题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
8.已知集合A={x|y=$\sqrt{2-x}}$},B={x|x2-2x<0},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
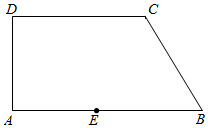 如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)
如图是一块直角梯形园地ABCD,AB∥CD,∠BAD=90°,经测最,AB=14m,CD=10m,∠ABC=60°,拟过线段AB上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),将该园地分为面积之比为3:1的左、石两部分分别种植不同花卉.设EB=x,EF=y(单位:m)